2024 AMC 10B Problems/Problem 1

The following problem is from both the 2024 AMC 10B #1 and 2024 AMC 12B #1, so both problems redirect to this page.

Problem

In a long line of people arranged left to right, the 1013th person from the left is also the 1010th person from the right. How many people are in line?

$\textbf{(A) } 2021 \qquad\textbf{(B) } 2022 \qquad\textbf{(C) } 2023 \qquad\textbf{(D) } 2024 \qquad\textbf{(E) } 2025$

Certain China Testpapers:

In a long line of people arranged left to right, the 1015th person from the left is also the 1010th person from the right. How many people are in line?

$\textbf{(A) } 2021 \qquad\textbf{(B) } 2022 \qquad\textbf{(C) } 2023 \qquad\textbf{(D) } 2024 \qquad\textbf{(E) } 2025$

Solution 1

If the person is the 1013th from the left, that means there is 1012 people to their left. If the person is the 1010th from the right, that means there is 1009 people to their right. Therefore, there are $1012 + 1 + 1009 = \boxed{\textbf{(B)} 2022}$ people in line.

Solution for certain China test papers:

If the person is the 1015th from the left, that means there is 1014 people to their left. If the person is the 1010th from the right, that means there is 1009 people to their right. Therefore, there are $1014 + 1 + 1009 = \boxed{\textbf{(D)} 2024}$ people in line.

~Aray10 (Main Solution) and RULE101 (Modifications for certain China test papers)

Solution 2

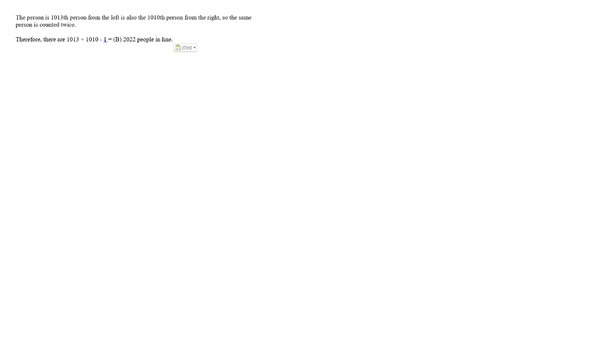
The person is 1013th person from the left is also the 1010th person from the right, so the same person is counted twice.

Therefore, there are 1013 + 1010 - 1 = $\boxed{\textbf{(B)} 2022}$ people in line.

~Kathan_17

Solution 3

We can look at a smaller case where it is the $4$ th person from the left and the $2$ nd person from the right. Listing out the people as numbers give us a list of $1,2,3,4,5.$ We see that the total number of people is the position from the left + the position from the right - 1 which in the case above is $4+2-1=5.$ Plugging in $1013$ and $1010$ gives us $1013+1010-1=\boxed{\textbf{(B)} 2022}$

~cownav

Video Solution 2 by SpreadTheMathLove

https://www.youtube.com/watch?v=24EZaeAThuE

2024 AMC 10B (Problems • Answer Key • Resources)
Preceded by First Problem	Followed by Problem 2
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

2024 AMC 12B (Problems • Answer Key • Resources)
Preceded by First Problem	Followed by Problem 2
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.

Page

Toolbox

Search