2024 AMC 12B Problems/Problem 13

Problem 13

There are real numbers $x,y,h$ and $k$ that satisfy the system of equations $x^2 + y^2 - 6x - 8y = h$ $x^2 + y^2 - 10x + 4y = k$ What is the minimum possible value of $h+k$ ?

$\textbf{(A) }-54 \qquad \textbf{(B) }-46 \qquad \textbf{(C) }-34 \qquad \textbf{(D) }-16 \qquad \textbf{(E) }16 \qquad$

Solution 1 (Easy and Fast)

Adding up the first and second equation, we get: $\begin{align*} h + k &= 2x^2 + 2y^2 - 16x - 4y \\ &= 2(x^2 - 8x) + 2(y^2 - 2y) \\ &= 2(x^2 - 8x) + 2(y^2 - 2y) \\ &= 2(x^2 - 8x + 16) - (2)(16) + 2(y^2 - 2y + 1) - (2)(1) \\ &= 2(x - 4)^2 + 2(y - 1)^2 - 34 \end{align*}$ All squared values must be greater than or equal to $0$ . As we are aiming for the minimum value, we set the two squared terms to be $0$ .

This leads to $\min(h + k) = 0 + 0 - 34 = \boxed{\textbf{(C)} -34}$

~mitsuihisashi14

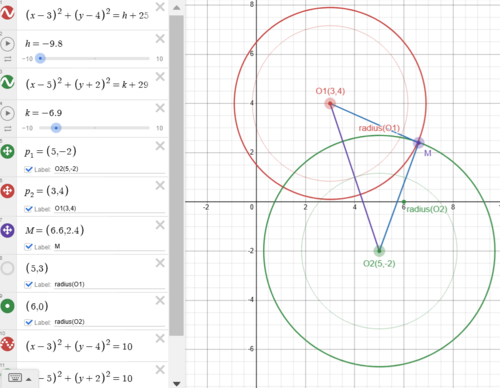
Solution 2 (Coordinate Geometry and AM-QM Inequality)

$(x-3)^2 + (y-4)^2 = h + 25$ $(x-5)^2 + (y+2)^2 = k + 29$ The distance between 2 circle centers is $(O_{1}O_{2})^2 = (5-3)^2 + (4 - (-2)) ^2 = 40$ The 2 circles must intersect given there exists one or more pairs of (x,y), connecting $O_{1}O_{2}$ and any pair of the 2 circle intersection points gives us a triangle with 3 sides, then $radius (O_{1}) + radius (O_{2}) \geq O_{1}O_{2}$ $\sqrt{h+25} + \sqrt{k+29} \geq 2\cdot\sqrt{10}$ Note that they will be equal if and only if the circles are tangent,

Applying the AM-QM inequality ( $2(a^2 + b^2) \geq (a+b)^2$ ) in the steps below, we get $h + k + 54 = (h + 25) + (k + 29) =\sqrt{(h + 25)}^2 + \sqrt{(k + 29)}^2 \geq \frac{\left(\sqrt{h + 25} + \sqrt{k + 29}\right)^2}{2} \geq \frac{\left(2\sqrt{10}\right)^2}{2} = 20.$

Therefore, $h + k \geq 20 - 54 = \boxed{C -34}$ .

~luckuso

Solution 3

~Kathan

Video Solution 1 by SpreadTheMathLove

https://www.youtube.com/watch?v=U0PqhU73yU0

2024 AMC 12B (Problems • Answer Key • Resources)
Preceded by Problem 12	Followed by Problem 14
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search