Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2024 AMC 10B Problems/Problem 1"

(→‎Problem)
m (I think it’s better to put the china problem in its own subsection)
 
(25 intermediate revisions by 14 users not shown)
Line 2: Line 2:
  
 
==Problem==
 
==Problem==
−
In a long line of people arranged left to right, the 1013th person from the left is also the 1010th person from the right. How many people are in line?
+
In a long line of people arranged left to right, the 1013th person from the left is also the 1010th person from the right. How many people are in the line?
  
 
<math>\textbf{(A) } 2021 \qquad\textbf{(B) } 2022 \qquad\textbf{(C) } 2023 \qquad\textbf{(D) } 2024 \qquad\textbf{(E) } 2025</math>
 
<math>\textbf{(A) } 2021 \qquad\textbf{(B) } 2022 \qquad\textbf{(C) } 2023 \qquad\textbf{(D) } 2024 \qquad\textbf{(E) } 2025</math>
Line 8: Line 8:
  
  
−
Certain China Testpapers:
+
===Modified Problem in Certain China Testpapers===
  
 
In a long line of people arranged left to right, the 1015th person from the left is also the 1010th person from the right. How many people are in line?
 
In a long line of people arranged left to right, the 1015th person from the left is also the 1010th person from the right. How many people are in line?
Line 26: Line 26:
  
 
~Aray10 (Main Solution) and RULE101 (Modifications for certain China test papers)
 
~Aray10 (Main Solution) and RULE101 (Modifications for certain China test papers)
 +
 +
==Solution 2==
 +
 +
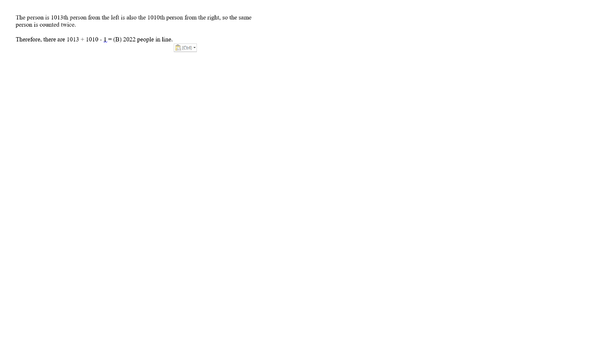
The person is <math>1013</math>rd person from the left is also the <math>1010</math>th person from the right, so the same person is counted twice.
 +
 +
Therefore, there are <math>1013+1010-1=\boxed{\textbf{(B)} 2022}</math> people in line.
 +
 +
~Kathan_17
 +
~megaboy6679
 +
[[Image: 2024_AMC_12B_P1.png|thumb|center|600px|]]
 +
 +
==Solution 3==
 +
We can look at a smaller case where it is the <math>4</math>th person from the left and the <math>2</math>nd person from the right. Listing out the people as numbers gives us a list of <math>1,2,3,4,5.</math> We see that the total number of people is the position from the left + the position from the right - 1, which in the case above is <math>4+2-1=5.</math> Plugging in <math>1013</math> and <math>1010</math> gives us <math>1013+1010-1=\boxed{\textbf{(B)} 2022}</math>
 +
 +
~cownav
 +
 +
==Solution 4==
 +
Since the person is the 1013th person from the left and the 1010th person from the right, there are 1009 people after the 1013th person.
 +
 +
Therefore, there are 1013 + 1009 = <math>\boxed{\textbf{(B)} 2022}</math> people in line.
 +
 +
(Note: Similarly, you can perceive this information as 1012 people to the left of 1010 people and proceed.)
 +
 +
~ElaineGu
 +
 +
==Video Solution 1 by SpreadTheMathLove==
 +
https://www.youtube.com/watch?v=24EZaeAThuE
 +
 +
== Video Solution 2 by Daily Dose of Math ==
 +
 +
https://youtu.be/XTUUEgYW_Fc
 +
 +
~Thesmartgreekmathdude
 +
 +
== Video Solution 3 (TheBeautyofMath) ==
 +
 +
https://www.youtube.com/watch?v=mpnm_r6D3-w
  
 
==See also==
 
==See also==
 
{{AMC10 box|year=2024|ab=B|before=First Problem|num-a=2}}
 
{{AMC10 box|year=2024|ab=B|before=First Problem|num-a=2}}
 
{{AMC12 box|year=2024|ab=B|before=First Problem|num-a=2}}
 
{{AMC12 box|year=2024|ab=B|before=First Problem|num-a=2}}
−
 
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 16:09, 19 November 2024

The following problem is from both the 2024 AMC 10B #1 and 2024 AMC 12B #1, so both problems redirect to this page.

Problem

In a long line of people arranged left to right, the 1013th person from the left is also the 1010th person from the right. How many people are in the line?

$\textbf{(A) } 2021 \qquad\textbf{(B) } 2022 \qquad\textbf{(C) } 2023 \qquad\textbf{(D) } 2024 \qquad\textbf{(E) } 2025$


Modified Problem in Certain China Testpapers

In a long line of people arranged left to right, the 1015th person from the left is also the 1010th person from the right. How many people are in line?

$\textbf{(A) } 2021 \qquad\textbf{(B) } 2022 \qquad\textbf{(C) } 2023 \qquad\textbf{(D) } 2024 \qquad\textbf{(E) } 2025$

Solution 1

If the person is the 1013th from the left, that means there is 1012 people to their left. If the person is the 1010th from the right, that means there is 1009 people to their right. Therefore, there are $1012 + 1 + 1009 = \boxed{\textbf{(B)} 2022}$ people in line.

Solution for certain China test papers:

If the person is the 1015th from the left, that means there is 1014 people to their left. If the person is the 1010th from the right, that means there is 1009 people to their right. Therefore, there are $1014 + 1 + 1009 = \boxed{\textbf{(D)} 2024}$ people in line.

~Aray10 (Main Solution) and RULE101 (Modifications for certain China test papers)

Solution 2

The person is $1013$rd person from the left is also the $1010$th person from the right, so the same person is counted twice.

Therefore, there are $1013+1010-1=\boxed{\textbf{(B)} 2022}$ people in line.

~Kathan_17 ~megaboy6679

2024 AMC 12B P1.png

Solution 3

We can look at a smaller case where it is the $4$th person from the left and the $2$nd person from the right. Listing out the people as numbers gives us a list of $1,2,3,4,5.$ We see that the total number of people is the position from the left + the position from the right - 1, which in the case above is $4+2-1=5.$ Plugging in $1013$ and $1010$ gives us $1013+1010-1=\boxed{\textbf{(B)} 2022}$

~cownav

Solution 4

Since the person is the 1013th person from the left and the 1010th person from the right, there are 1009 people after the 1013th person.

Therefore, there are 1013 + 1009 = $\boxed{\textbf{(B)} 2022}$ people in line.

(Note: Similarly, you can perceive this information as 1012 people to the left of 1010 people and proceed.)

~ElaineGu

Video Solution 1 by SpreadTheMathLove

https://www.youtube.com/watch?v=24EZaeAThuE

Video Solution 2 by Daily Dose of Math

https://youtu.be/XTUUEgYW_Fc

~Thesmartgreekmathdude

Video Solution 3 (TheBeautyofMath)

https://www.youtube.com/watch?v=mpnm_r6D3-w

See also

2024 AMC 10B (Problems • Answer Key • Resources)
Preceded by
First Problem 		Followed by
Problem 2
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
2024 AMC 12B (Problems • Answer Key • Resources)
Preceded by
First Problem 		Followed by
Problem 2
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2024_AMC_10B_Problems/Problem_1&oldid=235051"