Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2022 AMC 10A Problems/Problem 23

Revision as of 17:55, 25 October 2023 by Math-x (talk | contribs) (→‎Video Solution by Math-X (Smart and Simple))
The following problem is from both the 2022 AMC 10A #23 and 2022 AMC 12A #20, so both problems redirect to this page.

Problem

Isosceles trapezoid $ABCD$ has parallel sides $\overline{AD}$ and $\overline{BC},$ with $BC < AD$ and $AB = CD.$ There is a point $P$ in the plane such that $PA=1, PB=2, PC=3,$ and $PD=4.$ What is $\tfrac{BC}{AD}?$

$\textbf{(A) }\frac{1}{4}\qquad\textbf{(B) }\frac{1}{3}\qquad\textbf{(C) }\frac{1}{2}\qquad\textbf{(D) }\frac{2}{3}\qquad\textbf{(E) }\frac{3}{4}$

Solution 1 (Reflections + Ptolemy's Theorem)

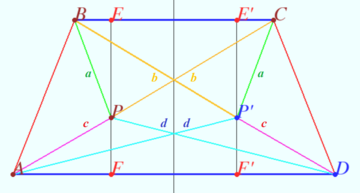
Consider the reflection $P^{\prime}$ of $P$ over the perpendicular bisector of $\overline{BC}$, creating two new isosceles trapezoids $DAPP^{\prime}$ and $CBPP^{\prime}$. Under this reflection, $P^{\prime}A=PD=4$, $P^{\prime}D=PA=1$, $P^{\prime}C=PB=2$, and $P^{\prime}B=PC=3$.

Since $DAPP'$ and $CBPP'$ are isosceles trapezoids, they are cyclic. Using Ptolemy's theorem on $DAPP'$, we get that $(PP')(AD) + (PA)(P'D) = (AP')(PD)$, so \[PP' \cdot AD + 1 \cdot 1 = 4 \cdot 4.\] Then, using Ptolemy's theorem again on $CBPP'$, we get that $(BC)(PP') + (BP)(CP') = (BP')(CP)$, so \[PP' \cdot BC + 2 \cdot 2 = 3 \cdot 3.\] Thus, $PP^{\prime}\cdot AD=15$ and $PP^{\prime}\cdot BC=5$; dividing these two equations and taking the reciprocal yields $\frac{BC}{AD}=\boxed{\textbf{(B) }\frac{1}{3}}$. [asy] size(300); pair A = (0,0); pair B = (1, 2); pair C = (2,2); pair D = (3,0); label("$A$", A, SW); label("$B$", B, NW); label("$C$", C, NE); label("$D$", D, SE); draw(A--B--C--D--cycle, blue); pair P = (0.8, 0.6); dot("$P$", P, NW); draw(P--A, magenta); draw(P--B, magenta); draw(P--C); draw(P--D); label("$1$", P--A, NW); label("$2$", P--B, E); label("$3$", P--C, NW); label("$4$", P--D, S); pair P1 = (2.2, 0.6); dot("$P'$", P1, NE); draw(P1--D, magenta); draw(P1--C, magenta); draw(P1--A); draw(P1--B); label("$1$", P1--D, NE); label("$2$", P1--C, E); label("$3$", P1--B, NE); label("$4$", P1--A, SE); draw(P--P1, dashed+magenta); [/asy] (diagram by cinnamon_e)

Solution 2 (Extensions + Stewart's Theorem)

[asy] size(7.5cm); draw((0,0)--(4.2,0)); draw((0,0)--(1.4,2)--(2.8,2)--(4.2,0)); draw((1.4,2)--(2.1,3)--(2.8,2)); draw((0,0)--(1,0.5)--(1.4,2)--(1,0.5)--(2.8,2)--(1,0.5)--(4.2,0)); label("$A$",(0,0),SW); label("$B$",(1.4,2),NW); label("$C$",(2.8,2),NE); label("$D$",(4.2,0),SE); label("$P$",(1,0.5),NW); label("$Q$",(2.1,3),N); draw((2.1,3)--(1,0.5)); [/asy]

Extend $AB$ and $CD$ to a point $Q$ as shown, and let $PQ = s$. Then let $BQ=CQ = a$ and $AB=DC = b$. Notice that $\frac{BC}{AD} = \frac{QC}{QD} = \frac{a}{a+b}$ by similar triangles.

By Stewart's theorem on $APQ$ and $DPQ$, we have \begin{align*} ab(a+b) + 9(a+b) &= 16a + s^2b \\ ab(a+b) + 4(a+b) &= a + s^2b \\ \end{align*}

Subtracting, $5(a+b) = 15a$, and so $\frac{BC}{AD} = \frac{a}{a+b} = \frac{5}{15} = \boxed{\textbf{(B) }\frac{1}{3}}$.

~kred9 (minor edit by gwang2008)

Solution 3 (Coordinate Bashing)

Since we're given distances and nothing else, we can represent each point as a coordinate and use the distance formula to set up a series of systems and equations. Let the height of the trapezoid be $h$, and let the coordinates of $A$ and $D$ be at $(-a,0)$ and $(a,0)$, respectively. Then let $B$ and $C$ be at $(-b,h)$ and $(b,h)$, respectively. This follows the rules that this is an isosceles trapezoid since the origin is centered on the middle of $AD$. Finally, let $P$ be located at point $(c,d)$.

The distance from $P$ to $A$ is $1$, so by the distance formula: \[\sqrt{(c+a)^2+(d-h)^2} = 1 \implies (c+a)^2+(d-h)^2 = 1\] The distance from $P$ to $D$ is $4$, so \[\sqrt{(c-a)^2+(d-h)^2} = 4 \implies (c-a)^2+(d-h)^2 = 16\]

Looking at these two equations alone, notice that the second term is the same for both equations, so we can subtract the equations. This yields \[-4ac = 15\]

Next, the distance from $P$ to $B$ is $2$, so \[\sqrt{(c+b)^2+(d-h)^2} = 2 \implies (c+b)^2+(d-h)^2 = 4\] The distance from $P$ to $C$ is $3$, so \[\sqrt{(c-b)^2+(d-h)^2} = 3 \implies (c-b)^2+(d-h)^2 = 9\]

Again, we can subtract these equations, yielding \[-4bc = 5\]

We can now divide the equations to eliminate $c$, yielding \[\frac{b}{a} = \frac{5}{15} = \frac{1}{3}\]

We wanted to find $\frac{BC}{AD}$. But since $b$ is half of $BC$ and $a$ is half of $AD$, this ratio is equal to the ratio we want.

Therefore $\frac{BC}{AD} = \boxed{\textbf{(B) }\frac{1}{3}}$.

~KingRavi

Solution 4 (Coordinate Bashing)

Let the point $P$ be at the origin, and draw four concentric circles around $P$ each with radius $1$, $2$, $3$, and $4$, respectively. The vertices of the trapezoid would be then on each of the four concentric circles. WLOG, let $BC$ and $AD$ be parallel to the x-axis. Assigning coordinates to each point, we have: \[A=(x_1,y_1)\] \[B=(x_2,y_2)\] \[C=(x_3,y_2)\] \[D=(x_4,y_1)\] which satisfy the following: \[x_1^2 + y_1^2 = 1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (1)\] \[x_2^2 + y_2^2 = 4 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (2)\] \[x_3^2 + y_2^2 = 9 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (3)\] \[x_4^2 + y_1^2 = 16 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (4)\] In addition, because the trapezoid is isosceles ($AB=CD$), the midpoints of the two bases would then have the same x-coordinate, giving us \[x_1 + x_4 = x_2 + x_3 \;\;\;\;\;\;\;\;\;\;\;\;\; (5)\] Subtracting Equation $2$ from Equation $3$, and Equation $1$ from Equation $4$, we have \[x_3^2 - x_2^2 = 5 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (6)\] \[x_4^2 - x_1^2 = 15 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (7)\] Dividing Equation $6$ by Equation $7$, we have \[\frac{x_3^2-x_2^2}{x_4^2-x_1^2}=\frac{1}{3}\] \[\frac{(x_3-x_2)(x_3+x_2)}{(x_4-x_1)(x_4+x_1)}=\frac{1}{3}.\] Cancelling $(x_3+x_2)$ and $(x_4+x_1)$ with Equation $5$, we get \[\frac{(x_3-x_2)}{(x_4-x_1)}=\frac{1}{3}.\] In other words, \[\frac{BC}{AD}=\frac{1}{3}=\boxed{\textbf{(B) }\frac{1}{3}}.\] ~G63566

Solution 5 (Cheese)

Notice that the question never says what the height of the trapezoid is; the only property we know about it is that $AC=BD$. Therefore, we can say WLOG that the height of the trapezoid is $0$ and all $5$ points, including $P$, lie on the same line with $PA=AB=BC=CD=1$. Notice that this satisfies the problem requirements because $PA=1, PB=2, PC=3,PD=4$, and $AC=BD=2$. Now all we have to find is $\frac{BC}{AD} = \boxed{\textbf{(B) }\frac{1}{3}}$.

~KingRavi

Solution 6 (Pythagorean Theorem)

2022 AMC 12A 24.png

Consider the reflection $P^{\prime}$ of $P$ over the perpendicular bisector of $\overline{BC}$. \[PB = P^{\prime}C = a, PC = P^{\prime}B = b.\] Let $PE \perp BC, P^{\prime}E^{\prime} \perp BC.$ \[BE = CE^{\prime}, PP^{\prime} = EE^{\prime} \implies\] \[b^2 - a^2 = PC^2 - PB^2 = CE^2 - BE^2\] \[=(CE - BE)(CE + BE) = EE^{\prime} \cdot BC = PP^{\prime} \cdot BC.\] Similarly, \[d^2 - c^2 = PP^{\prime} \cdot AD \implies \frac {BC}{AD} = \frac {b^2 - a^2}{d^2 - c^2}= \boxed{\textbf{(B) }\frac{1}{3}}.\] vladimir.shelomovskii@gmail.com, vvsss

Video Solution by Math-X (Smart and Simple)

https://youtu.be/7yAh4MtJ8a8?si=DZJywiBKH7yK97Hw&t=6149 ~Math-X

Video Solution by OmegaLearn

https://youtu.be/jnm2alniaM4

~ pi_is_3.14

Video Solution By ThePuzzlr

https://youtu.be/KqtpaHy-eoU

~ MathIsChess

Video Solution by Punxsutawney Phil

https://youtube.com/watch?v=uYXtEzX4fb0

Video Solution by Steven Chen

https://youtu.be/hvIOvjjQvIw

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Video Solution by MRENTHUSIASM (English & Chinese)

https://youtu.be/OXlyX-WzMfg

~MRENTHUSIASM

See also

2022 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 22 		Followed by
Problem 24
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
2022 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 19 		Followed by
Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2022_AMC_10A_Problems/Problem_23&oldid=200196"