Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1971 Canadian MO Problems/Problem 1"

m
Line 11: Line 11:
 
* [[1971 Canadian MO Problems/Problem 2|Next Problem]]
 
* [[1971 Canadian MO Problems/Problem 2|Next Problem]]
 
* [[1971 Canadian MO Problems|Back to Exam]]
 
* [[1971 Canadian MO Problems|Back to Exam]]
 +
 +
[[Category:Intermediate Geometry Problems]]

Revision as of 22:31, 27 July 2006

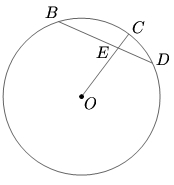
Problem

$\displaystyle DEB$ is a chord of a circle such that $\displaystyle DE=3$ and $\displaystyle EB=5 .$ Let $\displaystyle O$ be the center of the circle. Join $\displaystyle OE$ and extend $\displaystyle OE$ to cut the circle at $\displaystyle C.$ Given $\displaystyle EC=1,$ find the radius of the circle

CanadianMO 1971-1.jpg

Solution

First, extend $\displaystyle CO$ to meet the circle at $\displaystyle P.$ Let the radius be $\displaystyle r.$ Applying power of a point, $\displaystyle (EP)(CE)=(BE)(ED)$ and $\displaystyle 2r-1=15.$ Hence, $\displaystyle r=8.$

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1971_Canadian_MO_Problems/Problem_1&oldid=8597"