Difference between revisions of "2022 AIME II Problems/Problem 9"

Revision as of 11:50, 20 May 2023

Problem

Let $\ell_A$ and $\ell_B$ be two distinct parallel lines. For positive integers $m$ and $n$ , distinct points $A_1, A_2, \allowbreak A_3, \allowbreak \ldots, \allowbreak A_m$ lie on $\ell_A$ , and distinct points $B_1, B_2, B_3, \ldots, B_n$ lie on $\ell_B$ . Additionally, when segments $\overline{A_iB_j}$ are drawn for all $i=1,2,3,\ldots, m$ and $j=1,\allowbreak 2,\allowbreak 3, \ldots, \allowbreak n$ , no point strictly between $\ell_A$ and $\ell_B$ lies on more than 1 of the segments. Find the number of bounded regions into which this figure divides the plane when $m=7$ and $n=5$ . The figure shows that there are 8 regions when $m=3$ and $n=2$ $[asy] import geometry; size(10cm); draw((-2,0)--(13,0)); draw((0,4)--(10,4)); label("$\ell_A$",(-2,0),W); label("$\ell_B$",(0,4),W); point A1=(0,0),A2=(5,0),A3=(11,0),B1=(2,4),B2=(8,4),I1=extension(B1,A2,A1,B2),I2=extension(B1,A3,A1,B2),I3=extension(B1,A3,A2,B2); draw(B1--A1--B2); draw(B1--A2--B2); draw(B1--A3--B2); label("$A_1$",A1,S); label("$A_2$",A2,S); label("$A_3$",A3,S); label("$B_1$",B1,N); label("$B_2$",B2,N); label("1",centroid(A1,B1,I1)); label("2",centroid(B1,I1,I3)); label("3",centroid(B1,B2,I3)); label("4",centroid(A1,A2,I1)); label("5",(A2+I1+I2+I3)/4); label("6",centroid(B2,I2,I3)); label("7",centroid(A2,A3,I2)); label("8",centroid(A3,B2,I2)); dot(A1); dot(A2); dot(A3); dot(B1); dot(B2); [/asy]$

Solution 1

We can use recursion to solve this problem:

1. Fix 7 points on $\ell_A$ , then put one point $B_1$ on $\ell_B$ . Now, introduce a function $f(x)$ that indicates the number of regions created, where x is the number of points on $\ell_B$ . For example, $f(1) = 6$ because there are 6 regions.

2. Now, put the second point $B_2$ on $\ell_B$ . Join $A_1~A_7$ and $B_2$ will create $7$ new regions (and we are not going to count them again), and split the existing regions. Let's focus on the spliting process: line segment formed between $B_2$ and $A_1$ intersect lines $\overline{B_1A_2}$ , $\overline{B_1A_3}$ , ..., $\overline{B_1A_7}$ at $6$ points $\Longrightarrow$ creating $6$ regions (we already count one region at first), then $5$ points $\Longrightarrow$ creating $5$ regions (we already count one region at first), 4 points, etc. So, we have: $f(2) = f(1) + 7 + (6+5+...+1) = 34.$

3. If you still need one step to understand this: $A_1~A_7$ and $B_3$ will still create $7$ new regions. Intersecting $\overline{A_2B_1}, \overline{A_2B_2};$ $\overline{A_3B_1}, \overline{A_3B_2};$ $...$ $\overline{A_7B_1}, \overline{A_7B_2}$ at $12$ points, creating $12$ regions, etc. Thus, we have: $f(3) = f(2)+7+(12+10+8+...+2)=34+7+6\cdot 7=83.$

Yes, you might already notice that: $f(n+1) = f(n)+7+(6+5+...+1)\cdot n = f(n) + 7 + 21n.$

5. (Finally) we have $f(4) = 153$ , and $f(5)=244$ . Therefore, the answer is $\boxed{244}$ .

Note: we could deduce a general formula of this recursion: $f(n+1)=f(n)+N_a+\frac{n\cdot (N_a) \cdot (N_a-1)}{2}$ , where $N_a$ is the number of points on $\ell_A$

Solution 2

We want to derive a general function $f(m,n)$ that indicates the number of bounded regions. Observing symmetry, we know this is a symmetric function about $m$ and $n$ . Now let's focus on $f(m+1, n)-f(m, n)$ , which is the difference caused by adding one point to the existing $m$ points of line $\ell_A$ . This new point, call it #m, when connected to point #1 on $\ell_B$ , crosses $m*(n-1)$ lines, thus making additional $m*(n-1)+1$ bounded regions; when connected to point #2 on $\ell_B$ , it crosses $m*(n-2)$ lines, thus making additional $m*(n-2)+1$ bounded regions; etc. By simple algebra/recursion methods, we see

$f(m+1, n)-f(m, n)=m*\frac{n(n-1)}{2} +n$

Notice $f(1,n)=n-1$ . Not very difficult to figure out:

$f(m, n)=\frac{m(m-1)n(n-1)}{4} +mn-1$

The fact that $f(3,2)=8$ makes us more confident about the formula. Now plug in $m=5, n=7$ , we get the final answer of $\boxed{244}$ .

Solution 3

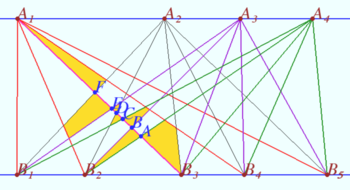
Let some number of segments be constructed. We construct a new segment. We start from the straight line $l_B.$ WLOG from point $B_3.$ Segment will cross several existing segments (points $A,B,C,...$ ) and enter one of the points of the line $l_A (A_1).$

Each of these points adds exactly 1 new bounded region (yellow bounded regions).

The exception is the only first segment $(A_1 B_1),$ which does not create any bounded region. Thus, the number of bounded regions is $1$ less than the number of points of intersection of the segments plus the number of points of arrival of the segments to $l_A.$

Each point of intersection of two segments is determined uniquely by the choice of pairs of points on each line.

The number of such pairs is $\dbinom{n}{2} \cdot \dbinom{m}{2}.$

Exactly one segment comes to each of the $n$ points of the line $l_A$ from each of the $m$ points of the line $l_B.$ The total number of arrivals is equal to $mn.$ Hence, the total number of bounded regions is $N = \dbinom{n}{2} \cdot \dbinom{m}{2} + mn – 1.$

We plug in $m=5, n=7$ , we get the final answer of $\boxed{244}$ .

vladimir.shelomovskii@gmail.com, vvsss

Solution 4 (Recursion with Detailed Explanation)

We use recursion for $2$ cases:

Case $1$ :

We add a new point on a line that already contains an equal number of points on lines $A$ and $B$ , we call the number $n$ . WLOG, let the point be on line $A$ . Then, it will have to connect to all the points on line $B$ . We observe that the number of new regions added for each line that connects the new point to some point on line $B$ is one more than the number of times the line from the new point to a point on line $B$ intersects another line formed by two arbitrary points on lines $A$ and $B$ which are not the new point. Therefore, we can focus on deriving a formula to find the number of intersections that will occur. We observe that the only way that a line chosen from two arbitrary points on lines $A$ and $B$ do not intersect with the line created from the new point to a point on line $B$ is if the line is formed by a point on line $B$ that is out of the "interval" in which the line created by the new point and the point on line $B$ go through. Therefore, if the new point connects to the furthest point on line $B$ , the number of lines that don't intersect will be the other lines formed by the point on line $B$ that connect to another point on line $A$ . Hence, the number of such lines is just $n$ , since that point on line $B$ can connect to any of the $x$ points on line $A$ which isn't the new point. Similarly, if the new point connects to the second furthest point on line $B$ , two points on line $B$ can form a line with any of the $n$ points on line $A$ . Generally, if the new point connects to the $x$ th furthest point on line $B$ , there will be $x\cdot{n}$ lines that don't intersect the line going through the new point and the $n$ th furthest point on line $B$ . We subtract the number of lines that never intersect with the new point and a point on line $B$ from the total number of possible lines. We can do this since we know that a point will not be in the intersection of $3$ or more lines. The equation for the total number of added regions across all possible lines can be modeled with $n^3-n\cdot\sum_{i=1}^{n}{i}+n\Longrightarrow n\cdot{(n^2-\sum_{i=1}^{n}{i}+1)}$

Case $2$ :

We add a point on line $B$ when there contains one more point on line $A$ then line $B$ . Following similar logic, each time that the new point connects to a point on line $A$ , the number of lines that don't intersect with the newly formed line from the new point to line $A$ is just the number of points on line $A$ that are out of the "interval" of that line multiplied by the number of points on line $B$ , which we will call $n$ if $n+1$ points are on line $A$ . Then, we can find the number of added regions using the equation $n\cdot{(n+1)^2}-n\cdot{\sum_{i=1}^{n+1}{i}+n+1}$ .

For the base case $x=2$ , the number of regions is $4$ . Therefore, all we need to do is plug in the values $x={3,4,5}$ for both formulas and apply $x=6$ for the first formula to find the number of regions when there are $6$ points on line $A$ and $5$ points on line $B$ . Next, we use the formula $n^2\cdot{n+1}-(n+1)\cdot\sum_{i=1}^{n}{i}+n$ to find the number of regions when there are $7$ points on line $A$ and $5$ points on line $B$ after adding a point on line $A$ again (This formula can be easily derived using the same method as above). After doing some calculations, we obtain the sum $8+9+12+22+28+45+55+65=\boxed{244}$

~Magnetoninja

Video Solution

https://youtu.be/OWNHkKlEo2A

~MathProblemSolvingSkills.com

@@ Line 87: / Line 87: @@
 Case <math>1</math>:
-We add a new point on a line that already contains an equal number of points on lines <math>A</math> and <math>B</math>, we call the number <math>x</math>. WLOG, let the point be on line <math>A</math>. Then, it will have to connect to all the points on line <math>B</math>. We observe that the number of new regions added for each line that connects the new point to some point on line <math>B</math> is one more than the number of times the line from the new point to a point on line <math>B</math> intersects another line formed by two arbitrary points on lines <math>A</math> and <math>B</math> which are not the new point. Therefore, we can focus on deriving a formula to find the number of intersections that will occur. We observe that the only way that a line chosen from two arbitrary points on lines <math>A</math> and <math>B</math> do not intersect with the line created from the new point to a point on line <math>B</math> is if the line is formed by a point on line <math>B</math> that is out of the "interval" in which the line created by the new point and the point on line <math>B</math> go through. Therefore, if the new point connects to the furthest point on line <math>B</math>, the number of lines that don't intersect will be the other lines formed by the point on line <math>B</math> that connect to another point on line <math>A</math>. Hence, the number of such lines is just <math>x</math>, since that point on line <math>B</math> can connect to any of the <math>x</math> points on line <math>A</math> which isn't the new point. Similarly, if the new point connects to the second furthest point on line <math>B</math>, two points on line <math>B</math> can form a line with any of the <math>x</math> points on line <math>A</math>. Generally, if the new point connects to the <math>n</math>th furthest point on line <math>B</math>, there will be <math>x\cdot{n}</math> lines that don't intersect the line going through the new point and the <math>n</math>th furthest point on line <math>B</math>. We subtract the number of lines that never intersect with the new point and a point on line <math>B</math> from the total number of possible lines. We can do this since we know that a point will not be in the intersection of <math>3</math> or more lines.
+We add a new point on a line that already contains an equal number of points on lines <math>A</math> and <math>B</math>, we call the number <math>n</math>. WLOG, let the point be on line <math>A</math>. Then, it will have to connect to all the points on line <math>B</math>. We observe that the number of new regions added for each line that connects the new point to some point on line <math>B</math> is one more than the number of times the line from the new point to a point on line <math>B</math> intersects another line formed by two arbitrary points on lines <math>A</math> and <math>B</math> which are not the new point. Therefore, we can focus on deriving a formula to find the number of intersections that will occur. We observe that the only way that a line chosen from two arbitrary points on lines <math>A</math> and <math>B</math> do not intersect with the line created from the new point to a point on line <math>B</math> is if the line is formed by a point on line <math>B</math> that is out of the "interval" in which the line created by the new point and the point on line <math>B</math> go through. Therefore, if the new point connects to the furthest point on line <math>B</math>, the number of lines that don't intersect will be the other lines formed by the point on line <math>B</math> that connect to another point on line <math>A</math>. Hence, the number of such lines is just <math>n</math>, since that point on line <math>B</math> can connect to any of the <math>x</math> points on line <math>A</math> which isn't the new point. Similarly, if the new point connects to the second furthest point on line <math>B</math>, two points on line <math>B</math> can form a line with any of the <math>n</math> points on line <math>A</math>. Generally, if the new point connects to the <math>x</math>th furthest point on line <math>B</math>, there will be <math>x\cdot{n}</math> lines that don't intersect the line going through the new point and the <math>n</math>th furthest point on line <math>B</math>. We subtract the number of lines that never intersect with the new point and a point on line <math>B</math> from the total number of possible lines. We can do this since we know that a point will not be in the intersection of <math>3</math> or more lines.
-The equation for the total number of added regions across all possible lines can be modeled with <math>x^3-x\cdot\sum_{i=1}^{x}{i}+x \Longrightarrow x\cdot{(x^2-\sum_{i=1}^{x}{i}+1)}</math>
+The equation for the total number of added regions across all possible lines can be modeled with <math>n^3-n\cdot\sum_{i=1}^{n}{i}+n\Longrightarrow n\cdot{(n^2-\sum_{i=1}^{n}{i}+1)}</math>
 Case <math>2</math>:

2022 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 8	Followed by Problem 10
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search