2022 AIME II Problems/Problem 11
Contents
Problem
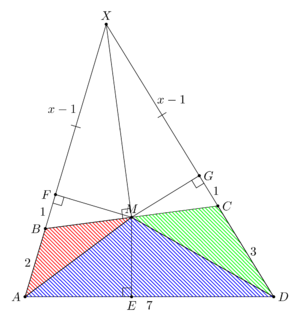
Let ![]() be a convex quadrilateral with
be a convex quadrilateral with ![]() and
and ![]() such that the bisectors of acute angles
such that the bisectors of acute angles ![]() and
and ![]() intersect at the midpoint of
intersect at the midpoint of ![]() Find the square of the area of
Find the square of the area of ![]()
Solution 1
![[asy] defaultpen(fontsize(12)+0.6); size(300); pair A,B,C,D,M,H; real xb=71, xd=121; A=origin; D=(7,0); B=2*dir(xb); C=3*dir(xd)+D; M=(B+C)/2; H=foot(M,A,D); path c=CR(D,3); pair A1=bisectorpoint(D,A,B), D1=bisectorpoint(C,D,A), Bp=IP(CR(A,2),A--H), Cp=IP(CR(D,3),D--H); draw(B--A--D--C--B); draw(A--M--D^^M--H^^Bp--M--Cp, gray+0.4); draw(rightanglemark(A,H,M,5)); dot("$A$",A,SW); dot("$D$",D,SE); dot("$B$",B,NW); dot("$C$",C,NE); dot("$M$",M,up); dot("$H$",H,down); dot("$B'$",Bp,down); dot("$C'$",Cp,down); [/asy]](http://latex.artofproblemsolving.com/b/9/f/b9f1648f98069bf13ca0fe7ea4d24ef9ecbf0de5.png)
According to the problem, we have ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]()
Because ![]() is the midpoint of
is the midpoint of ![]() , we have
, we have ![]() , so:
, so: ![]()
Then, we can see that ![]() is an isosceles triangle with
is an isosceles triangle with ![]()
Therefore, we could start our angle chasing: ![]() .
.
This is when we found that points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are on a circle. Thus,
are on a circle. Thus, ![]() . This is the time we found that
. This is the time we found that ![]() .
.
Thus, ![]()
Point ![]() is the midpoint of
is the midpoint of ![]() , and
, and ![]() .
. ![]() .
.
The area of this quadrilateral is the sum of areas of triangles: ![]()
![]()
![]()
![]()
Finally, the square of the area is ![]()
Solution 2
Denote by ![]() the midpoint of segment
the midpoint of segment ![]() .
Let points
.
Let points ![]() and
and ![]() be on segment
be on segment ![]() , such that
, such that ![]() and
and ![]() .
.
Denote ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Denote ![]() . Because
. Because ![]() is the midpoint of
is the midpoint of ![]() ,
, ![]() .
.
Because ![]() is the angle bisector of
is the angle bisector of ![]() and
and ![]() ,
, ![]() .
Hence,
.
Hence, ![]() and
and ![]() .
Hence,
.
Hence, ![]() .
.
Because ![]() is the angle bisector of
is the angle bisector of ![]() and
and ![]() ,
, ![]() .
Hence,
.
Hence, ![]() and
and ![]() .
Hence,
.
Hence, ![]() .
.
Because ![]() is the midpoint of segment
is the midpoint of segment ![]() ,
, ![]() .
Because
.
Because ![]() and
and ![]() ,
, ![]() .
.
Thus, ![]() .
.
Thus,
![]()
In ![]() ,
, ![]() .
In addition,
.
In addition, ![]() .
Thus,
.
Thus,
![]()
Taking ![]() , we get
, we get ![]() .
Taking
.
Taking ![]() , we get
, we get ![]() .
.
Therefore, ![]() .
.
Hence, ![]() and
and ![]() .
Thus,
.
Thus, ![]() and
and ![]() .
.
In ![]() , by applying the law of cosines,
, by applying the law of cosines, ![]() .
Hence,
.
Hence, ![]() .
Hence,
.
Hence, ![]() .
.
Therefore,

Therefore, the square of ![]() is
is ![]() .
.
~Steven Chen (www.professorchenedu.com)
Solution 3 (Visual)
Claim
In the triangle ![]() is the midpoint of
is the midpoint of ![]() is the point of intersection of the circumcircle and the bisector of angle
is the point of intersection of the circumcircle and the bisector of angle ![]() Then
Then ![]()
Proof
Let ![]() Then
Then ![]()
Let ![]() be the intersection point of the perpendicular dropped from
be the intersection point of the perpendicular dropped from ![]() to
to ![]() with the circle.
with the circle.
Then the sum of arcs ![]()
![]()
Let ![]() be the point of intersection of the line
be the point of intersection of the line ![]() with the circle.
with the circle.
![]() is perpendicular to
is perpendicular to ![]() the sum of arcs
the sum of arcs ![]() coincides with
coincides with ![]()
The inscribed angles ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]()
Solution
Let ![]() and
and ![]() on
on ![]()
Then ![]()
Quadrilateral ![]() is cyclic.
Let
is cyclic.
Let ![]() Then
Then ![]()
Circle ![]() centered at
centered at ![]() is its diameter,
is its diameter, ![]()
![]() since they both complete
since they both complete ![]() to
to ![]()
![]() since they are the exterior angles of an isosceles
since they are the exterior angles of an isosceles ![]()
![]() by two angles.
by two angles.
![]()
The height dropped from ![]() to
to ![]() is
is ![]()
The areas of triangles ![]() and
and ![]() are equal to
are equal to ![]() area of
area of ![]() is
is ![]()
![]() The area of
The area of ![]() is
is ![]()
vladimir.shelomovskii@gmail.com, vvsss
Solution 4 (THINK OUTSIDE THE BOX)
Extend ![]() and
and ![]() so they intersect at a point
so they intersect at a point ![]() . Then note that
. Then note that ![]() is the incenter of
is the incenter of ![]() , implying that
, implying that ![]() is on the angle bisector of
is on the angle bisector of ![]() . Now because
. Now because ![]() is both an angle bisector and a median of
is both an angle bisector and a median of ![]() ,
, ![]() is isosceles. Then we can start angle chasing:
is isosceles. Then we can start angle chasing:
Let ![]() and
and ![]() . Then
. Then ![]() , implying that
, implying that ![]() , implying that
, implying that ![]() , or that
, or that ![]() . Substituting this into the rest of the diagram, we find that
. Substituting this into the rest of the diagram, we find that ![]() .
.
Then ![]() , or
, or ![]() . Moreover,
. Moreover, ![]() , or
, or ![]() . Similarly,
. Similarly, ![]() , or
, or ![]() . Then using Law of Cosines on
. Then using Law of Cosines on ![]() , to get that
, to get that ![]() , or
, or ![]() .
.
We finish by using the formula ![]() , as follows:
, as follows:
![]() .
.
![]() .
.
-dragoon
Solution 5 (incircle)
As shown in paragraph one of solution 4, extending ![]() and
and ![]() to
to ![]() , we realize that
, we realize that ![]() is isosceles, thus
is isosceles, thus ![]() . Let
. Let ![]() . And, midpoint
. And, midpoint ![]() is the incenter of
is the incenter of ![]() . Construct perpendiculars
. Construct perpendiculars ![]() to sides
to sides ![]() respectively (constructing the radii of the incircle). Let
respectively (constructing the radii of the incircle). Let ![]() . The semiperimeter
. The semiperimeter ![]() . Since
. Since ![]() is the tangent off the incircle,
is the tangent off the incircle, ![]() . So,
. So, ![]() . Because
. Because ![]() ,
,
![]() .
.
By Heron's formula and the inradius area formula,
![]()
Then, ![]() . Finally,
. Finally,
![]()
Thus, our answer is ![]()
Remark
![]() and
and ![]() are the tangent points of the X-mixtilinear incircle (of
are the tangent points of the X-mixtilinear incircle (of ![]() ). This may be useful, but I haven't looked into it.
). This may be useful, but I haven't looked into it.
Solution 6 (bash)
Let the midpoint of ![]() be
be ![]() . Angle-chase and observe that
. Angle-chase and observe that ![]() . Let
. Let ![]() and
and ![]() and
and ![]() . As a result of this similarity, we write
. As a result of this similarity, we write
![]()
which gives ![]() . Similarly, we write
. Similarly, we write
![]()
and
![]()
to get ![]() and
and ![]() .
.
We now have all required side lengths; we can find the area of ![]() with Heron's formula. Doing so yields
with Heron's formula. Doing so yields ![]() . We could also bash out the areas of the other two triangles since we know all their side lengths (this is what I did :sob:), but a more intelligent method is to recall the triangles' similarity. The ratio of similarlity between
. We could also bash out the areas of the other two triangles since we know all their side lengths (this is what I did :sob:), but a more intelligent method is to recall the triangles' similarity. The ratio of similarlity between ![]() and
and ![]() is
is ![]() , and between
, and between ![]() and
and ![]() is
is ![]() . Thus, the area ratios are
. Thus, the area ratios are ![]() and
and ![]() , respectively, so adding together we have
, respectively, so adding together we have ![]() . Multiplying this by our
. Multiplying this by our ![]() , we have
, we have ![]() as their total area. Adding this to our original area, we have
as their total area. Adding this to our original area, we have ![]() .
.
The square of this is ![]() .
.
~~Technodoggo
Solution 7 (similar to 4)
As in solution 4, let ![]() , so
, so ![]() is the incenter of
is the incenter of ![]() and
and ![]() . Let
. Let ![]() . Then the normalized barycentric coordinates of
. Then the normalized barycentric coordinates of ![]() ,
, ![]() , and
, and ![]() with respect to
with respect to ![]() are
are ![]() ,
, ![]() , and
, and ![]() . So we have
. So we have ![]() giving
giving ![]() . The sidelengths of
. The sidelengths of ![]() are thus
are thus ![]() ,
, ![]() , and
, and ![]() giving
giving ![]() . Also, we have
. Also, we have ![]() so that
so that ![]() . The area squared is thus
. The area squared is thus ![]() .
~~ golue3120
.
~~ golue3120
Video Solution by The Power of Logic
See Also
| 2022 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()