Difference between revisions of "2022 AMC 10A Problems/Problem 25"
(→See Also) |
(→See Also) |
||
| Line 16: | Line 16: | ||
== See Also == | == See Also == | ||
| − | {{AMC10 box|year=2022|ab=A|num-b=24}} | + | {{AMC10 box|year=2022|ab=A|num-b=24|num-b=1}} |
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 15:09, 12 November 2022
Problem 25
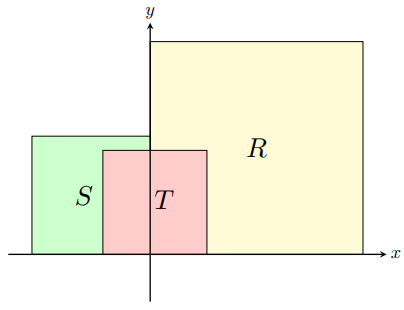
Let 
, 
, and 
be squares that have vertices at lattice points (i.e., points whose coordinates are both integers) in the coordinate plane, together with their interiors. The bottom edge of each square is on the x-axis. The left edge of and the right edge of are on the 
-axis, and contains 
as many lattice points as does . The top two vertices of are in 
, and contains 
of the lattice points contained in . See the figure (not drawn to scale).
The fraction of lattice points in that are in 
is 27 times the fraction of lattice points in that are in 
. What is the minimum possible value of the edge length of plus the edge length of plus the edge length of ?
Solution
Solution in progress
~KingRavi
See Also
| 2022 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 1 |
Followed by [[2022 AMC 10A Problems/Problem {{{num-a}}}|Problem {{{num-a}}}]] | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
