Difference between revisions of "2006 AMC 12A Problems/Problem 6"
I_like_pie (talk | contribs) (Added Image) |
I_like_pie (talk | contribs) (Added Image #2 and small changes) |
||
| Line 9: | Line 9: | ||
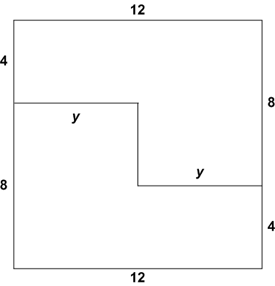
Since the two [[hexagon]]s are going to be repositioned to form a [[square (geometry) | square]] without overlap, the [[area]] will remain the same. The rectangle's area is <math>18\cdot8=144</math>. This means the square will have four sides of length 12. The only way to do this is shown below.<br> | Since the two [[hexagon]]s are going to be repositioned to form a [[square (geometry) | square]] without overlap, the [[area]] will remain the same. The rectangle's area is <math>18\cdot8=144</math>. This means the square will have four sides of length 12. The only way to do this is shown below.<br> | ||
| − | [[Image: | + | [[Image:2006 AMC 12A Problem 6 - Solution.png]] |
| − | As you can see from the diagram, the [[line segment]] denoted as <math>y</math> is | + | As you can see from the diagram, the [[line segment]] denoted as <math>y</math> is half the length of the side of the square, which leads to <math>y</math><math> = \frac{12}{2} = 6 \Longrightarrow \mathrm{(A)}</math>. |
== See also == | == See also == | ||
Revision as of 19:52, 15 September 2007
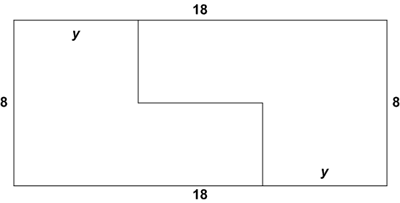
Problem
The 
rectangle 
is cut into two congruent hexagons, as shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is 
?
Solution
Since the two hexagons are going to be repositioned to form a square without overlap, the area will remain the same. The rectangle's area is 
. This means the square will have four sides of length 12. The only way to do this is shown below.
As you can see from the diagram, the line segment denoted as is half the length of the side of the square, which leads to 
.
See also
| 2006 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 5 |
Followed by Problem 7 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
