Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2005 AMC 10A Problems/Problem 23"

m (→‎Solution 1)
m (→‎Solution 2)
Line 42: Line 42:
  
 
Since <math>m\angle DCO=m\angle DFC=90^\circ</math>, then <math>\triangle DCO\cong \triangle DFC</math>. So the ratio of the two altitudes is <math>\frac{CF}{DC}=\frac{OC}{DO}=\frac{1}{3}\Rightarrow \text{(C)}</math>
 
Since <math>m\angle DCO=m\angle DFC=90^\circ</math>, then <math>\triangle DCO\cong \triangle DFC</math>. So the ratio of the two altitudes is <math>\frac{CF}{DC}=\frac{OC}{DO}=\frac{1}{3}\Rightarrow \text{(C)}</math>
 +
 +
==Solution 3==
 +
 +
Say the center of the circle is point F;
 +
Without loss of generality, assume <math>AC=2</math>, so <math>CB=4</math> and the diameter and radius are <math>6</math> and <math>3</math>, respectively. Therefore, <math>CF=1</math> and <math>DF=3</math>.
 +
The area of <math>\triangle CDE</math> can be expressed as <math>\frac{1}{2}(CD)(2r)sin(CDE)</math>, where <math>r</math> is the radius of circle <math>F</math>. <math>\frac{1}{2}(CD)(2r)</math> happens to be the area of <math>\triangle ADB</math>. Furthermore, <math>sin CDE = \frac{CF}{DF},</math> or <math>\frac{1}{3}.</math> Therefore, the ratio is <math>\frac{1}{3}.</math>
  
 
==See also==
 
==See also==

Revision as of 12:46, 14 September 2015

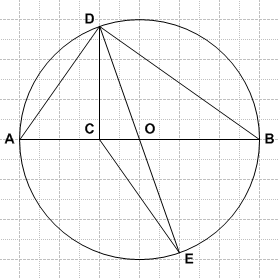
Problem

Let $AB$ be a diameter of a circle and let $C$ be a point on $AB$ with $2\cdot AC=BC$. Let $D$ and $E$ be points on the circle such that $DC \perp AB$ and $DE$ is a second diameter. What is the ratio of the area of $\triangle DCE$ to the area of $\triangle ABD$?

$\mathrm{(A) \ } \frac{1}{6}\qquad \mathrm{(B) \ } \frac{1}{4}\qquad \mathrm{(C) \ } \frac{1}{3}\qquad \mathrm{(D) \ } \frac{1}{2}\qquad \mathrm{(E) \ } \frac{2}{3}$

Solution 1

Circlenc1.png

Let us assume that the diameter is of length $1$.

$AC$ is $\frac{1}{3}$ of diameter and $CO$ is $\frac{1}{2}-\frac{1}{3} = \frac{1}{6}$.

$OD$ is the radius of the circle, so using the Pythagorean theorem height $CD$ of $\triangle AOC$ is $\sqrt{(\frac{1}{2})^2-(\frac{1}{6})^2} = \frac{\sqrt{2}}{3}$. This is also the height of the $\triangle ABD$.

Area of the $\triangle DCO$ is $\frac{1}{2}\cdot\frac{1}{6}\cdot\frac{\sqrt{2}}{3}$ = $\frac{\sqrt{2}}{36}$.

The height of $\triangle DCE$ can be found using the area of $\triangle DCO$ and $DO$ as base.

Hence the height of $\triangle DCE$ is $\frac{\frac{\sqrt{2}}{36}}{\frac{1}{2}\cdot\frac{1}{2}}$ = $\frac{\sqrt{2}}{9}$.

The diameter is the base for both the triangles $\triangle DCE$ and $\triangle ABD$.

Hence, the ratio of the area of $\triangle DCE$ to the area of $\triangle ABD$ is $\frac{\frac{\sqrt{2}}{9}}{\frac{\sqrt{2}}{3}}$ = $\frac{1}{3} \Rightarrow C$

Solution 2

Since $\triangle DCE$ and $\triangle ABD$ share a base, the ratio of their areas is the ratio of their altitudes. Draw the altitude from $C$ to $DE$.

[asy] import graph; import olympiad; pair O,A,B,C,D,E,F; O=(0,0);A=(15,0);B=(-15,0);C=(5,0);D=(5,14.142135623730950488016887242097);E=(-5,-14.142135623730950488016887242097);F=(0.5555555555555555,1.5713484026367722764463208046774); draw(Circle((0,0),15)); draw(A--B);draw(D--E);draw(C--D);draw(C--E);draw(C--F);draw(A--D);draw(D--B); label("A",A,NE);label("B",B,W);label("C",C,SE);label("D",D,NE);label("E",E,SW);label("O",O,SW);label("F",F,NW); markscalefactor=0.2; draw(anglemark(C,F,D),blue);draw(anglemark(D,C,B),blue); [/asy] $OD=r, OC=\frac{1}{3}r$.

Since $m\angle DCO=m\angle DFC=90^\circ$, then $\triangle DCO\cong \triangle DFC$. So the ratio of the two altitudes is $\frac{CF}{DC}=\frac{OC}{DO}=\frac{1}{3}\Rightarrow \text{(C)}$

Solution 3

Say the center of the circle is point F; Without loss of generality, assume $AC=2$, so $CB=4$ and the diameter and radius are $6$ and $3$, respectively. Therefore, $CF=1$ and $DF=3$. The area of $\triangle CDE$ can be expressed as $\frac{1}{2}(CD)(2r)sin(CDE)$, where $r$ is the radius of circle $F$. $\frac{1}{2}(CD)(2r)$ happens to be the area of $\triangle ADB$. Furthermore, $sin CDE = \frac{CF}{DF},$ or $\frac{1}{3}.$ Therefore, the ratio is $\frac{1}{3}.$

See also

2005 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 22 		Followed by
Problem 24
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2005_AMC_10A_Problems/Problem_23&oldid=72061"