Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2005 AMC 10A Problems/Problem 23

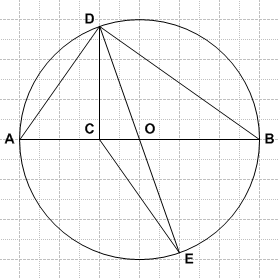
Problem

Let $AB$ be a diameter of a circle and let $C$ be a point on $AB$ with $2\cdot AC=BC$. Let $D$ and $E$ be points on the circle such that $DC \perp AB$ and $DE$ is a second diameter. What is the ratio of the area of $\triangle DCE$ to the area of $\triangle ABD$?

[asy] unitsize(2.5cm); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=3; pair O=(0,0), C=(-1/3,0), B=(1,0), A=(-1,0); pair D=dir(aCos(C.x)), E=(-D.x,-D.y); draw(A--B--D--cycle); draw(D--E--C); draw(unitcircle,white); drawline(D,C); dot(O); clip(unitcircle); draw(unitcircle); label("$E$",E,SSE); label("$B$",B,E); label("$A$",A,W); label("$D$",D,NNW); label("$C$",C,SW); draw(rightanglemark(D,C,B,2));[/asy]

$\textbf{(A) } \frac{1}{6}\qquad \textbf{(B) } \frac{1}{4}\qquad \textbf{(C) } \frac{1}{3}\qquad \textbf{(D) } \frac{1}{2}\qquad \textbf{(E) } \frac{2}{3}$

Solution 1

Circlenc1.png

WLOG, let us assume that the diameter is of length $1$.

The length of $AC$ is $\frac{1}{3}$ and $CO$ is $\frac{1}{2}-\frac{1}{3} = \frac{1}{6}$.

$OD$ is the radius of the circle, which is $\frac{1}{2}$, so using the Pythagorean Theorem the height $CD$ of $\triangle DCO$ is $\sqrt{\left(\frac{1}{2}\right)^2-\left(\frac{1}{6}\right)^2} = \frac{\sqrt{2}}{3}$. This is also the height of the $\triangle ABD$.

The area of $\triangle DCO$ is $\frac{1}{2}\cdot\frac{1}{6}\cdot\frac{\sqrt{2}}{3}$ = $\frac{\sqrt{2}}{36}$.

The height of $\triangle DCE$ can be found using the area of $\triangle DCO$ and $DO$ as base.

Hence, the height of $\triangle DCE$ is $\dfrac{\dfrac{\sqrt{2}}{36}}{\dfrac{1}{2}\cdot\dfrac{1}{2}}$ = $\dfrac{\sqrt{2}}{9}$.

The diameter is the base for both the triangles $\triangle DCE$ and $\triangle ABD$,

Hence, the ratio of the area of $\triangle DCE$ to the area of $\triangle ABD$ is $\dfrac{\dfrac{\sqrt{2}}{9}}{\dfrac{\sqrt{2}}{3}}$ = $\boxed{\textbf{(C) }\frac{1}{3}}$

Solution 2

Since $\triangle DCE$ and $\triangle ABD$ share a base, the ratio of their areas is the ratio of their altitudes. Draw the altitude from $C$ to $DE$.

[asy] import graph; import olympiad; pair O,A,B,C,D,E,F; O=(0,0);A=(15,0);B=(-15,0);C=(5,0);D=(5,14.142135623730950488016887242097);E=(-5,-14.142135623730950488016887242097);F=(0.5555555555555555,1.5713484026367722764463208046774); draw(Circle((0,0),15)); draw(A--B);draw(D--E);draw(C--D);draw(C--E);draw(C--F);draw(A--D);draw(D--B); label("A",A,NE);label("B",B,W);label("C",C,SE);label("D",D,NE);label("E",E,SW);label("O",O,SW);label("F",F,NW); markscalefactor=0.2; draw(anglemark(C,F,D),blue);draw(anglemark(D,C,B),blue); [/asy] $OD=r, OC=\frac{1}{3}r$.

Since $m\angle DCO=m\angle DFC=90^\circ$, then $\triangle DCO\sim \triangle DFC$. So the ratio of the two altitudes is $\frac{CF}{DC}=\frac{OC}{DO}=\boxed{\textbf{(C) }\frac{1}{3}}$

Solution 3

Let the center of the circle be point $O$; Without loss of generality, assume $AC=2$, so $CB=4$ and the diameter and radius are $6$ and $3$, respectively. Therefore, $CO=1$, and $DO=3$. The area of $\triangle DCE$ can be expressed as $\frac{1}{2}(CD)(6)\text{sin }(CDE).$ $\frac{1}{2}(CD)(6)$ happens to be the area of $\triangle ABD$. Furthermore, $\text{sin } CDE = \frac{CO}{DO},$ or $\frac{1}{3}.$ Therefore, the ratio is $\boxed{\textbf{(C) }\frac{1}{3}}.$

Solution 4

[asy] unitsize(2.5cm); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=3; pair O=(0,0), C=(-1/3.0), B=(1,0), A=(-1,0); pair D=dir(aCos(C.x)), E=(-D.x,-D.y); draw(A--B--D--cycle); draw(D--E--C); draw(unitcircle,white); drawline(D,C); dot(O); clip(unitcircle); draw(unitcircle); label("$E$",E,SSE); label("$B$",B,E); label("$A$",A,W); label("$D$",D,NNW); label("$C$",C,SW); draw(rightanglemark(D,C,B,2)); [/asy]


Let the point G be the reflection of point $D$ across $\overline{AB}$. (Point G is on the circle).


Let $AC=x$, then $BC=2x$. The diameter is $3x$. To find $DC$, there are two ways (presented here):

1. Since $\overline{AB}$ is the diameter, $CD=CG$. Using power of points, \[AC\cdot BC=x\cdot2x=2x^{2}=CD^{2} \longrightarrow CD=x\sqrt{2}\] 2. Use the geometric mean theorem, \[AC\cdot BC=x\cdot2x=2x^{2}=CD^{2} \longrightarrow CD=x\sqrt{2}\] (These are the same equations but obtained through different formulae)


Therefore $DG=2x\sqrt{2}$. Since $\overline{DE}$ is a diameter, $\triangle DGE$ is right. By the Pythagorean theorem, \[DE^{2}=GD^{2}+GE^{2} \longrightarrow \left(3x\right)^{2}=\left(2x\sqrt{2}\right)^{2}+GE^{2}\] \[9x^{2}=8x^{2}+GE^{2} \longrightarrow GE^{2}=x^{2} \longrightarrow GE=x\]


As established before, $\angle DGE$ is right (if you are unsure, look up "inscribed angle theorem", this is a special case of the theorem where the central angle measures $180^{\circ}$) so $GE=x$ is the altitude of $\triangle DCE$, and $DC=x\sqrt{2}$ is the base. Therefore \[\left[DCE\right]=\frac{1}{2}\cdot DC\cdot GE=\frac{1}{2}\cdot x\sqrt{2}\cdot x=\frac{x^{2}\sqrt{2}}{2}\]


$AB=3x$ is the base of $\triangle ABD$ and $CD=x\sqrt{2}$ is the height. \[\left[ABD\right]=\frac{1}{2}\cdot3x\cdot x\sqrt{2}=\frac{3x^{2}\sqrt{2}}{2}\]


The required ratio is \[\frac{\left[DCE\right]}{\left[ABD\right]}=\frac{\frac{x^{2}\sqrt{2}}{2}}{\frac{3x^{2}\sqrt{2}}{2}}=\frac{x^{2}\sqrt{2}}{2}\cdot\frac{2}{3x^{2}\sqrt{2}}=\frac{x^{2}\sqrt{2}}{3x^{2}\sqrt{2}}=\frac{1}{3}\] The answer is $\boxed{\textbf{(C) } \frac{1}{3}}$.


~JH. L

Solution 5

Assume the diameter is $3$.

$AC = 1$

Get the height $CD = \sqrt{(AC)(BC)} = \sqrt2$ via power of a point.

$CO = AO - AC = 1/2$.

By altitude of right triangle $\triangle CDO$: Altitude from $C$ to $DE$ is same as altitude from $C$ to $DO$ is $\frac{(CO)(CD)}{DO} = \frac{(1/2)(\sqrt2)}{\frac 3 2}$.

$\triangle DCE$ and $\triangle ABD$ have the same (diameter) hypotenuse length, so their area ratio is their altitude ratio is $\frac {\frac{ (1/2)(\sqrt2) } {\frac 3 2}} {\sqrt2} = \boxed{1/3}$.

~oinava

Video solution

https://youtu.be/i6eooSSJF64

See Also

2005 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 22 		Followed by
Problem 24
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2005_AMC_10A_Problems/Problem_23&oldid=233223"