Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2006 AMC 12A Problems/Problem 16"

(→‎See also)
Line 10: Line 10:
 
[[Image:2006_AMC12A-16a.png]]
 
[[Image:2006_AMC12A-16a.png]]
  
−
<math>\angle AEC</math> and <math>\angle BED</math> are [[vertical angles]] so they are [[congruent (geometry) | congruent]], as are [[angle]]s <math>\angle ACE</math> and <math>\angle BDE</math> (both are [[right angle]]s because the radius and [[tangent line]] at a point on a circle are always [[perpendicular]]). Thus, <math>\triangle ACE \sim \triangle BDE</math>.
+
<math>\angle AEC</math> and <math>\angle BED</math> are [[vertical angles]] so they are [[congruent (geometry) | congruent]], as are [[angle]]s <math>\angle ADE</math> and <math>\angle BCE</math> (both are [[right angle]]s because the radius and [[tangent line]] at a point on a circle are always [[perpendicular]]). Thus, <math>\triangle ACE \sim \triangle BDE</math>.
  
−
By the [[Pythagorean Theorem]], [[line segment]] <math>DE = 4</math>.  The sides are [[proportion]]al, so <math>\frac{CE}{AC} = \frac{DE}{BD} \Rightarrow \frac{4}{3} = \frac{DE}{8}</math>. This makes <math>DE = \frac{32}{3}</math> and <math>CD = CE + DE = 4 + \frac{32}{3} = \frac{44}{3} \Longrightarrow \mathrm{B}</math>.
+
By the [[Pythagorean Theorem]], [[line segment]] <math>DE = 4</math>.  The sides are [[proportion]]al, so <math>\frac{DE}{AD} = \frac{CE}{BC} \Rightarrow \frac{4}{3} = \frac{CE}{8}</math>. This makes <math>CE = \frac{32}{3}</math> and <math>CD = CE + DE = 4 + \frac{32}{3} = \frac{44}{3} \Longrightarrow \mathrm{B}</math>.
  
 
== See also ==
 
== See also ==

Revision as of 16:46, 26 January 2014

The following problem is from both the 2006 AMC 12A #16 and 2006 AMC 10A #23, so both problems redirect to this page.

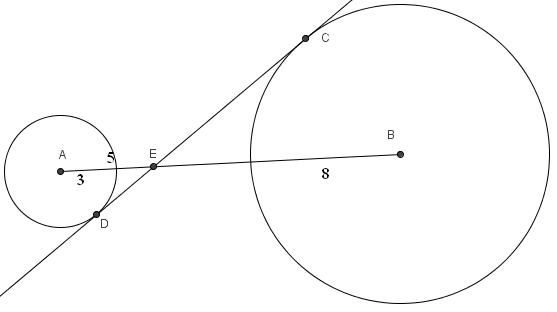
Problem

Circles with centers $A$ and $B$ have radii 3 and 8, respectively. A common internal tangent intersects the circles at $C$ and $D$, respectively. Lines $AB$ and $CD$ intersect at $E$, and $AE=5$. What is $CD$?

$\mathrm{(A) \ } 13\qquad\mathrm{(B) \ } \frac{44}{3}\qquad\mathrm{(C) \ } \sqrt{221}\qquad\mathrm{(D) \ } \sqrt{255}\qquad\mathrm{(E) \ } \frac{55}{3}\qquad$

2006 AMC12A-16.png

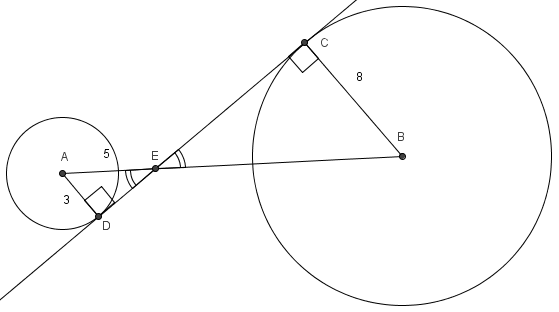
Solution

2006 AMC12A-16a.png

$\angle AEC$ and $\angle BED$ are vertical angles so they are congruent, as are angles $\angle ADE$ and $\angle BCE$ (both are right angles because the radius and tangent line at a point on a circle are always perpendicular). Thus, $\triangle ACE \sim \triangle BDE$.

By the Pythagorean Theorem, line segment $DE = 4$. The sides are proportional, so $\frac{DE}{AD} = \frac{CE}{BC} \Rightarrow \frac{4}{3} = \frac{CE}{8}$. This makes $CE = \frac{32}{3}$ and $CD = CE + DE = 4 + \frac{32}{3} = \frac{44}{3} \Longrightarrow \mathrm{B}$.

See also

2006 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 15 		Followed by
Problem 17
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions
2006 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 22 		Followed by
Problem 24
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_AMC_12A_Problems/Problem_16&oldid=58889"