Difference between revisions of "2007 AMC 8 Problems/Problem 11"
(→Solution) |
(→Solution) |
||
| Line 40: | Line 40: | ||
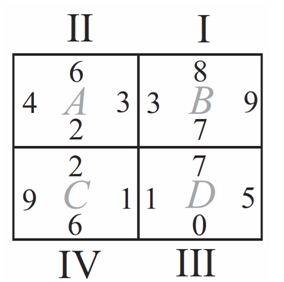
We first notice that tile III has a <math>0</math> on the bottom and a <math>5</math> on the right side. Since no other tile has a <math>0</math> or a <math>5</math>, Tile III must be in rectangle <math>D</math>. Tile III also has a <math>1</math> on the left, so Tile IV must be in Rectangle <math>C</math>. | We first notice that tile III has a <math>0</math> on the bottom and a <math>5</math> on the right side. Since no other tile has a <math>0</math> or a <math>5</math>, Tile III must be in rectangle <math>D</math>. Tile III also has a <math>1</math> on the left, so Tile IV must be in Rectangle <math>C</math>. | ||
| − | The answer is <math>\boxed{\textbf{(D)} | + | The answer is <math>\boxed{\textbf{(D)}}</math> |
<center>[[Image:AMC8_2007_11S.png]]</center> | <center>[[Image:AMC8_2007_11S.png]]</center> | ||
Revision as of 12:19, 9 December 2012
Problem
Tiles 
and 
are translated so one tile coincides with each of the rectangles 
and 
. In the final arrangement, the two numbers on any side common to two adjacent tiles must be the same. Which of the tiles is translated to Rectangle 
?
![[asy] size(400); defaultpen(linewidth(0.8)); path p=origin--(8,0)--(8,6)--(0,6)--cycle; draw(p^^shift(8.5,0)*p^^shift(8.5,10)*p^^shift(0,10)*p); draw(shift(20,2)*p^^shift(28,2)*p^^shift(20,8)*p^^shift(28,8)*p); label("8", (4,6+10), S); label("6", (4+8.5,6+10), S); label("7", (4,6), S); label("2", (4+8.5,6), S); label("I", (4,6+10), N); label("II", (4+8.5,6+10), N); label("III", (4,6), N); label("IV", (4+8.5,6), N); label("3", (0,3+10), E); label("4", (0+8.5,3+10), E); label("1", (0,3), E); label("9", (0+8.5,3), E); label("7", (4,10), N); label("2", (4+8.5,10), N); label("0", (4,0), N); label("6", (4+8.5,0), N); label("9", (8,3+10), W); label("3", (8+8.5,3+10), W); label("5", (8,3), W); label("1", (8+8.5,3), W); label("A", (24,10), N); label("B", (32,10), N); label("C", (24,4), N); label("D", (32,4), N);[/asy]](http://latex.artofproblemsolving.com/7/e/7/7e7f71699fece62a1150cc80613baf59935980df.png)
cannot be determined
Solution
We first notice that tile III has a 
on the bottom and a 
on the right side. Since no other tile has a or a , Tile III must be in rectangle . Tile III also has a 
on the left, so Tile IV must be in Rectangle .
The answer is 
See Also
| 2007 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
