Difference between revisions of "2006 AMC 12A Problems/Problem 16"
(get rid of extra template) |
|||
| Line 15: | Line 15: | ||
== See also == | == See also == | ||
{{AMC12 box|year=2006|ab=A|num-b=15|num-a=17}} | {{AMC12 box|year=2006|ab=A|num-b=15|num-a=17}} | ||
| + | |||
| + | {{AMC10 box|year=2006|ab=A|num-b=22|num-a=24}} | ||
[[Category:Introductory Geometry Problems]] | [[Category:Introductory Geometry Problems]] | ||
Revision as of 21:25, 1 December 2007
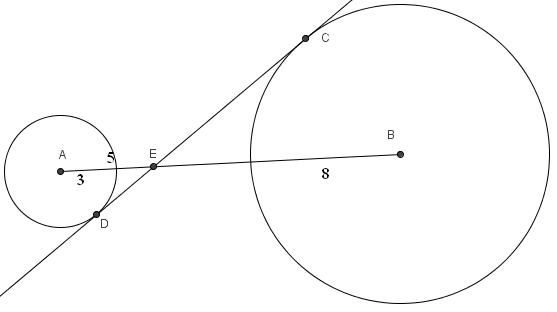
Problem
Circles with centers 
and 
have radii 3 and 8, respectively. A common internal tangent intersects the circles at 
and 
, respectively. Lines 
and 
intersect at 
, and 
. What is ?
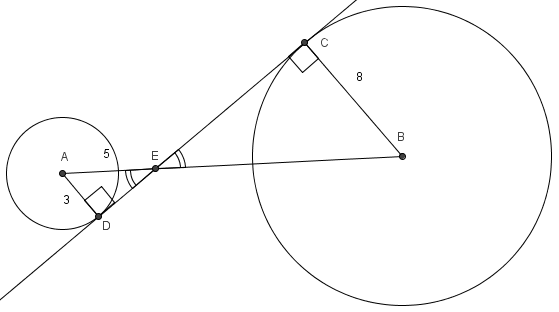
Solution
and 
are vertical angles so they are congruent, as are angles 
and 
(both are right angles because the radius and tangent line at a point on a circle are always perpendicular). Thus, 
.
By the Pythagorean Theorem, line segment 
. The sides are proportional, so 
. This makes 
and 
.
See also
| 2006 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 15 |
Followed by Problem 17 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
| 2006 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 22 |
Followed by Problem 24 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
