Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2022 AIME II Problems/Problem 9"

(→‎Solution 2)
(→‎Solution 3)
Line 63: Line 63:
  
 
==Solution 3==
 
==Solution 3==
−
 
+
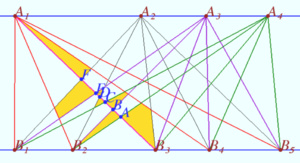
[[File:AIME 2022 II 9-min.png|300px|right]]
  
 
Let some number of segments be constructed. We construct a new segment. We start from the straight line <math>l_B.</math> WLOG from point <math>B_3.</math>  Segment will cross several existing segments (points <math>A,B,C,...</math>) and enter one of the points of the line  <math>l_A (A_1).</math>
 
Let some number of segments be constructed. We construct a new segment. We start from the straight line <math>l_B.</math> WLOG from point <math>B_3.</math>  Segment will cross several existing segments (points <math>A,B,C,...</math>) and enter one of the points of the line  <math>l_A (A_1).</math>
Line 72: Line 72:
 
Thus, the number of bounded regions is <math>1</math> less than the number of points of intersection of the segments plus the number of points of arrival of the segments to <math>l_A.</math>
 
Thus, the number of bounded regions is <math>1</math> less than the number of points of intersection of the segments plus the number of points of arrival of the segments to <math>l_A.</math>
  
−
Each point of intersection of two segments is determined <i><b> uniquely</b></i> by the choice of pairs of points on each line. The number of such pairs is Cn2 Cm2.
+
Each point of intersection of two segments is determined <i><b> uniquely</b></i> by the choice of pairs of points on each line.  
 +
 
 +
The number of such pairs is Cn2 Cm2.
 
Exactly one segment comes to each of the n points of the line lA from each of the m points of the line lB. The total number of arrivals is equal to mn.
 
Exactly one segment comes to each of the n points of the line lA from each of the m points of the line lB. The total number of arrivals is equal to mn.
 
Hence, the total number of bounded regions is N = Cn2 Cm2 + mn – 1.
 
Hence, the total number of bounded regions is N = Cn2 Cm2 + mn – 1.

Revision as of 13:02, 1 June 2022

Problem

Let $\ell_A$ and $\ell_B$ be two distinct parallel lines. For positive integers $m$ and $n$, distinct points $A_1, A_2, \allowbreak A_3, \allowbreak \ldots, \allowbreak A_m$ lie on $\ell_A$, and distinct points $B_1, B_2, B_3, \ldots, B_n$ lie on $\ell_B$. Additionally, when segments $\overline{A_iB_j}$ are drawn for all $i=1,2,3,\ldots, m$ and $j=1,\allowbreak 2,\allowbreak 3, \ldots, \allowbreak n$, no point strictly between $\ell_A$ and $\ell_B$ lies on more than two of the segments. Find the number of bounded regions into which this figure divides the plane when $m=7$ and $n=5$. The figure shows that there are 8 regions when $m=3$ and $n=2$. [asy] import geometry; size(10cm); draw((-2,0)--(13,0)); draw((0,4)--(10,4)); label("$\ell_A$",(-2,0),W); label("$\ell_B$",(0,4),W); point A1=(0,0),A2=(5,0),A3=(11,0),B1=(2,4),B2=(8,4),I1=extension(B1,A2,A1,B2),I2=extension(B1,A3,A1,B2),I3=extension(B1,A3,A2,B2); draw(B1--A1--B2); draw(B1--A2--B2); draw(B1--A3--B2); label("$A_1$",A1,S); label("$A_2$",A2,S); label("$A_3$",A3,S); label("$B_1$",B1,N); label("$B_2$",B2,N); label("1",centroid(A1,B1,I1)); label("2",centroid(B1,I1,I3)); label("3",centroid(B1,B2,I3)); label("4",centroid(A1,A2,I1)); label("5",(A2+I1+I2+I3)/4); label("6",centroid(B2,I2,I3)); label("7",centroid(A2,A3,I2)); label("8",centroid(A3,B2,I2)); dot(A1); dot(A2); dot(A3); dot(B1); dot(B2); [/asy]

Solution 1

We can use recursion to solve this problem:

1. Fix 7 points on $\ell_A$, then put one point $B_1$ on $\ell_B$. Now, introduce a function $f(x)$ that indicates the number of regions created, where x is the number of points on $\ell_B$. For example, $f(1) = 6$ because there are 6 regions.

2. Now, put the second point $B_2$ on $\ell_B$. Join $A_1~A_7$ and $B_2$ will create $7$ new regions (and we are not going to count them again), and split the existing regions. Let's focus on the spliting process: line segment formed between $B_2$ and $A_1$ intersect lines $\overline{B_1A_2}$, $\overline{B_1A_3}$, ..., $\overline{B_1A_7}$ at $6$ points $\Longrightarrow$ creating $6$ regions (we already count one region at first), then $5$ points $\Longrightarrow$ creating $5$ regions (we already count one region at first), 4 points, etc. So, we have: \[f(2) = f(1) + 7 + (6+5+...+1) = 34.\]

3. If you still need one step to understand this: $A_1~A_7$ and $B_3$ will still create $7$ new regions. Intersecting \[\overline{A_2B_1}, \overline{A_2B_2};\] \[\overline{A_3B_1}, \overline{A_3B_2};\] \[...\] \[\overline{A_7B_1}, \overline{A_7B_2}\] at $12$ points, creating $12$ regions, etc. Thus, we have: \[f(3) = f(2)+7+(12+10+8+...+2)=34+7+6\cdot 7=83.\]

Yes, you might already notice that: \[f(n+1) = f(n)+7+(6+5+...+1)\cdot n = f(n) + 7 + 21n.\]

5. (Finally) we have $f(4) = 153$, and $f(5)=244$. Therefore, the answer is $\boxed{244}$.

Note: we could deduce a general formula of this recursion: $f(n+1)=f(n)+N_a+\frac{n\cdot (N_a) \cdot (N_a-1)}{2}$, where $N_a$ is the number of points on $\ell_A$.

~DSAERF-CALMIT (https://binaryphi.site)

Solution 2

We want to derive a general function $f(m,n)$ that indicates the number of bounded regions. Observing symmetry, we know this is a symmetric function about $m$ and $n$. Now let's focus on $f(m+1, n)-f(m, n)$, which is the difference caused by adding one point to the existing $m$ points of line $\ell_A$. This new point, call it #m, when connected to point #1 on $\ell_B$, crosses $m*(n-1)$ lines, thus making additional $m*(n-1)+1$ bounded regions; when connected to point #2 on $\ell_B$, it crosses $m*(n-2)$ lines, thus making additional $m*(n-2)+1$ bounded regions; etc. By simple algebra/recursion methods, we see

$f(m+1, n)-f(m, n)=m*\frac{n(n-1)}{2} +n$

Notice $f(1,n)=n-1$. Not very difficult to figure out:

$f(m, n)=\frac{m(m-1)n(n-1)}{4} +mn-1$

The fact that $f(3,2)=8$ makes us more confident about the formula. Now plug in $m=5, n=7$, we get the final answer of $\boxed{244}$.

Solution 3

AIME 2022 II 9-min.png

Let some number of segments be constructed. We construct a new segment. We start from the straight line $l_B.$ WLOG from point $B_3.$ Segment will cross several existing segments (points $A,B,C,...$) and enter one of the points of the line $l_A (A_1).$

Each of these points adds exactly 1 new bounded region (yellow bounded regions).

The exception is the only first segment $(A_1 B_1),$ which does not create any bounded region. Thus, the number of bounded regions is $1$ less than the number of points of intersection of the segments plus the number of points of arrival of the segments to $l_A.$

Each point of intersection of two segments is determined uniquely by the choice of pairs of points on each line.

The number of such pairs is Cn2 Cm2. Exactly one segment comes to each of the n points of the line lA from each of the m points of the line lB. The total number of arrivals is equal to mn. Hence, the total number of bounded regions is N = Cn2 Cm2 + mn – 1.

We plug in $m=5, n=7$, we get the final answer of $\boxed{244}$. ~vvsss (www.deoma-cmd.ru)

See Also

2022 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 8 		Followed by
Problem 10
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2022_AIME_II_Problems/Problem_9&oldid=174214"