Difference between revisions of "1971 Canadian MO Problems/Problem 1"
m (wikified) |
(→Solution) |
||
| (9 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
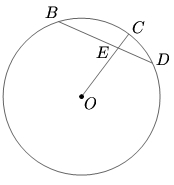
| − | <math> | + | <math>DEB</math> is a chord of a circle such that <math>DE=3</math> and <math>EB=5 .</math> Let <math>O</math> be the center of the circle. Join <math>OE</math> and extend <math>OE</math> to cut the circle at <math>C.</math> Given <math>EC=1,</math> find the radius of the circle. |
[[Image:CanadianMO_1971-1.jpg]] | [[Image:CanadianMO_1971-1.jpg]] | ||
== Solution == | == Solution == | ||
| − | First, extend <math> | + | First, extend <math>CO</math> to meet the circle at <math>P.</math> Let the radius be <math>r.</math> Applying [[power of a point]], |
| − | <math> | + | <math>(EP)(CE)=(BE)(ED)</math> and <math>2r-1=15.</math> Hence, <math>r=8.</math> |
| − | - | + | == See Also == |
| − | + | {{Old CanadaMO box|before=First Question|num-a=2|year=1971}} | |
| − | + | ||
| + | [[Category:Intermediate Geometry Problems]] | ||
Latest revision as of 15:33, 4 September 2024
Problem
is a chord of a circle such that 
and 
Let 
be the center of the circle. Join 
and extend to cut the circle at 
Given 
find the radius of the circle.
Solution
First, extend 
to meet the circle at 
Let the radius be 
Applying power of a point,
and 
Hence, 
See Also
| 1971 Canadian MO (Problems) | ||
| Preceded by First Question |
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • | Followed by Problem 2 |
