Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1994 AIME Problems/Problem 14"

(→‎Solution)
(→‎Solution)
 
(8 intermediate revisions by 5 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
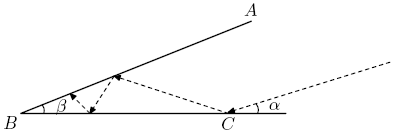
A beam of light strikes <math>\overline{BC}\,</math> at point <math>C\,</math> with angle of incidence <math>\alpha=19.94^\circ\,</math> and reflects with an equal angle of reflection as shown.  The light beam continues its path, reflecting off line segments <math>\overline{AB}\,</math> and <math>\overline{BC}\,</math> according to the rule: angle of incidence equals angle of reflection.  Given that <math>\beta=\alpha/10=1.994^\circ\,</math> and <math>AB=AC,\,</math> determine the number of times the light beam will bounce off the two line segments.  Include the first reflection at <math>C\,</math> in your count.
+
A beam of light strikes <math>\overline{BC}\,</math> at point <math>C\,</math> with angle of incidence <math>\alpha=19.94^\circ\,</math> and reflects with an equal angle of reflection as shown.  The light beam continues its path, reflecting off line segments <math>\overline{AB}\,</math> and <math>\overline{BC}\,</math> according to the rule: angle of incidence equals angle of reflection.  Given that <math>\beta=\alpha/10=1.994^\circ\,</math> and <math>AB=BC,\,</math> determine the number of times the light beam will bounce off the two line segments.  Include the first reflection at <math>C\,</math> in your count.
  
 
[[Image:AIME_1994_Problem_14.png]]
 
[[Image:AIME_1994_Problem_14.png]]
  
 
== Solution ==
 
== Solution ==
−
=== Solution 1 ===
 
 
At each point of reflection, we pretend instead that the light continues to travel straight.  
 
At each point of reflection, we pretend instead that the light continues to travel straight.  
−
 
 
<asy>
 
<asy>
 
pathpen = linewidth(0.7); size(250);  
 
pathpen = linewidth(0.7); size(250);  
 
real alpha = 28, beta = 36;  
 
real alpha = 28, beta = 36;  
−
pair B = D(MP("B",(0,0))), C = MP("C",D((1,0))), A = MP("A",D(expi(alpha * pi/180)),N); path r = C + .4 * expi(beta * pi/180) -- C - 2*expi(beta * pi/180);  
+
pair B = MP("B",(0,0),NW), C = MP("C",D((1,0))), A = MP("A",expi(alpha * pi/180),N); path r = C + .4 * expi(beta * pi/180) -- C - 2*expi(beta * pi/180);  
−
D(A--B--(1.5,0));D(r);D(anglemark(C,B,A));D(anglemark((1.5,0),C,C+.4*expi(beta*pi/180)));MP("\beta",B,(5,1.2),fontsize(9));MP("\alpha",C,(4,1.2),fontsize(9));
+
D(A--B--(1.5,0));D(r);D(anglemark(C,B,D(A)));D(anglemark((1.5,0),C,C+.4*expi(beta*pi/180)));MP("\beta",B,(5,1.2),fontsize(9));MP("\alpha",C,(4,1.2),fontsize(9));
 
for(int i = 0; i < 180/alpha; ++i){
 
for(int i = 0; i < 180/alpha; ++i){
 
  path l = B -- (1+i/2)*expi(-i * alpha * pi / 180);
 
  path l = B -- (1+i/2)*expi(-i * alpha * pi / 180);
 
  D(l, linetype("4 4"));
 
  D(l, linetype("4 4"));
 
  D(IP(l,r));
 
  D(IP(l,r));
−
}
+
} D(B);
 
</asy>
 
</asy>
−
 
+
Note that after <math>k</math> reflections (excluding the first one at <math>C</math>) the extended line will form an angle <math>k \beta</math> at point <math>B</math>. For the <math>k</math>th reflection to be just inside or at point <math>B</math>, we must have <math>k\beta \le 180 - 2\alpha \Longrightarrow k \le \frac{180 - 2\alpha}{\beta} = 70.27</math>. Thus, our answer is, including the first intersection, <math>\left\lfloor \frac{180 - 2\alpha}{\beta} \right\rfloor + 1 = \boxed{071}</math>.
−
Then each intersection of the extended line with the rotated segments corresponds to a reflection in the original problem. We quickly see that the extended line will intersect each rotation of the angle by <math>k \beta</math> until <math>k\beta \ge 180 - \alpha \Longrightarrow k \ge \frac{180 - \alpha}{\beta}</math>. Thus, our answer is, including the first intersection, <math>\left\lceil \frac{180 - \alpha}{\beta} \right\rceil = \boxed{081}</math>.
 
−
 
 
−
=== Solution 2 ===
 
−
Same as above except, the last paragraph of the above solution needs correction.
 
−
 
 
−
Note that after k reflections (excluding the first one at <math>C</math>) the extended line will form an angle <math>k \beta</math> at point <math>B</math>. For the <math>k</math>th reflection to be just inside or at the point <math>C</math>, we must have <math>k\beta \le 180 - 2\alpha \Longrightarrow k \le \frac{180 - 2\alpha}{\beta} = 70.27</math>. Thus, our answer is, including the first intersection, <math>\left\lfloor \frac{180 - 2\alpha}{\beta} \right\rfloor + 1 = \boxed{071}</math>.
 
  
 
== See also ==
 
== See also ==
Line 31: Line 23:
  
 
[[Category:Intermediate Geometry Problems]]
 
[[Category:Intermediate Geometry Problems]]
 +
{{MAA Notice}}

Latest revision as of 23:03, 27 December 2017

Problem

A beam of light strikes $\overline{BC}\,$ at point $C\,$ with angle of incidence $\alpha=19.94^\circ\,$ and reflects with an equal angle of reflection as shown. The light beam continues its path, reflecting off line segments $\overline{AB}\,$ and $\overline{BC}\,$ according to the rule: angle of incidence equals angle of reflection. Given that $\beta=\alpha/10=1.994^\circ\,$ and $AB=BC,\,$ determine the number of times the light beam will bounce off the two line segments. Include the first reflection at $C\,$ in your count.

AIME 1994 Problem 14.png

Solution

At each point of reflection, we pretend instead that the light continues to travel straight. [asy] pathpen = linewidth(0.7); size(250); real alpha = 28, beta = 36; pair B = MP("B",(0,0),NW), C = MP("C",D((1,0))), A = MP("A",expi(alpha * pi/180),N); path r = C + .4 * expi(beta * pi/180) -- C - 2*expi(beta * pi/180); D(A--B--(1.5,0));D(r);D(anglemark(C,B,D(A)));D(anglemark((1.5,0),C,C+.4*expi(beta*pi/180)));MP("\beta",B,(5,1.2),fontsize(9));MP("\alpha",C,(4,1.2),fontsize(9)); for(int i = 0; i < 180/alpha; ++i){ path l = B -- (1+i/2)*expi(-i * alpha * pi / 180); D(l, linetype("4 4")); D(IP(l,r)); } D(B); [/asy] Note that after $k$ reflections (excluding the first one at $C$) the extended line will form an angle $k \beta$ at point $B$. For the $k$th reflection to be just inside or at point $B$, we must have $k\beta \le 180 - 2\alpha \Longrightarrow k \le \frac{180 - 2\alpha}{\beta} = 70.27$. Thus, our answer is, including the first intersection, $\left\lfloor \frac{180 - 2\alpha}{\beta} \right\rfloor + 1 = \boxed{071}$.

See also

1994 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 13 		Followed by
Problem 15
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1994_AIME_Problems/Problem_14&oldid=89223"