Difference between revisions of "2025 AMC 8 Problems/Problem 21"
| (One intermediate revision by one other user not shown) | |||
| Line 7: | Line 7: | ||
the sum of the grade levels assigned to pods <math>C, E</math>, and <math>F</math>? | the sum of the grade levels assigned to pods <math>C, E</math>, and <math>F</math>? | ||
| − | [[Image:2025_AMC_8_problem_21.png| | + | [[Image:2025_AMC_8_problem_21.png|center]] |
<math>\textbf{(A)}~12\qquad\textbf{(B)}~13\qquad\textbf{(C)}~14\qquad\textbf{(D)}~15\qquad\textbf{(E)}~16</math> | <math>\textbf{(A)}~12\qquad\textbf{(B)}~13\qquad\textbf{(C)}~14\qquad\textbf{(D)}~15\qquad\textbf{(E)}~16</math> | ||
| Line 39: | Line 39: | ||
~hsnacademy | ~hsnacademy | ||
| + | ==Video Solution by Dr. David== | ||
| + | https://youtu.be/OF3kt3zuYf0 | ||
== See Also == | == See Also == | ||
Latest revision as of 19:21, 2 February 2025
Contents
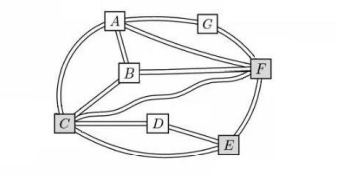
Problem
The Konigsberg School has assigned grades 1 through 7 to pods 
through 
, one grade per
pod. Some of the pods are connected by walkways, as shown in the figure below. The school
noticed that each pair of connected pods has been assigned grades differing by 2 or more grade
levels. (For example, grades 1 and 2 will not be in pods directly connected by a walkway.) What is
the sum of the grade levels assigned to pods 
, and 
?
Solution 1
The key observation for this solution is to observe that pods 
and both have degree 5; that is, they are connected to five other pods. This implies that and must contain grades 1 and 7 in either order (if or contained any of grades 2, 3, 4, 5, or 6, then there would only be four possible grades for five pods, a contradiction). It does not matter which grade and gets (see Solution 2 below), so we will assume that pod is assigned grade 1, and pod is assigned grade 7.
Next, pod 
is the only pod which is not adjacent to pod , so pod must be assigned grade 6. Similarly, pod must be assigned grade 2.
Lastly, we need to assign grades 3, 4, and 5 to pods , 
, and 
. Note that and are adjacent; therefore, pods and must contain grades 3 and 5. We conclude that must be assigned grade 4. The requested sum is 
.
Solution 2 (Fast)
Suppose that we replaced each label 
with 
. That is, we replaced the grade 
assigned to with the grade 
, the grade 
assigned to with 
, and so on. We claim that if the initial labeling is valid (i.e., each pair of connected pods has grades differing by 2 or more), then so will the new labeling. This follows as if 
, then 
. This shows that if there is an assignment 
of grades to the pods, where 
, then there is a second, valid assignment.
Because this is an AMC 8 problem and only one answer is correct, we can conclude that 
. Simplifying and solving for 
gives 
.
-scrabbler94
Video Solution 1 by Thinking Feet
Video Solution 2 in Less Than 2 Minutes by Dr. Xue's Math School
This is our first video posted on the AoPS website. Our goal is to help students learn more efficiently.
Video Solution (A Clever Explanation You’ll Get Instantly)
https://youtu.be/VP7g-s8akMY?si=qVENFSXALJsh0DvX&t=2948 ~hsnacademy
Video Solution by Dr. David
See Also
| 2025 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 20 |
Followed by Problem 22 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
