Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2006 AMC 12A Problems/Problem 22"

(→‎Problem)
(→‎Solution)
 
(6 intermediate revisions by 5 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
 
 
A [[circle]] of [[radius]] <math>r</math> is [[concentric]] with and outside a [[regular polygon | regular]] [[hexagon]] of side length <math>2</math>. The [[probability]] that three entire sides of hexagon are visible from a randomly chosen point on the circle is <math>1/2</math>. What is <math>r</math>?
 
A [[circle]] of [[radius]] <math>r</math> is [[concentric]] with and outside a [[regular polygon | regular]] [[hexagon]] of side length <math>2</math>. The [[probability]] that three entire sides of hexagon are visible from a randomly chosen point on the circle is <math>1/2</math>. What is <math>r</math>?
  
−
<math> \mathrm{(A) \ } 2\sqrt{2}+2\sqrt{3}\qquad \mathrm{(B) \ } 3\sqrt{3}+\sqrt{2}\qquad \rm{(C) \ } 2\sqrt{6}+\sqrt{3}\qquad \rm{(D) \ } 3\sqrt{2}+\sqrt{6}</math>
+
<math> \mathrm{(A) \ } 2\sqrt{2}+2\sqrt{3}\qquad \mathrm{(B) \ } 3\sqrt{3}+\sqrt{2}\qquad \mathrm{(C) \ } 2\sqrt{6}+\sqrt{3}\qquad \rm{(D) \ } 3\sqrt{2}+\sqrt{6}\qquad \mathrm{(E) \ }  6\sqrt{2}-\sqrt{3}</math>
−
 
 
−
<math>\mathrm{(E) \ }  6\sqrt{2}-\sqrt{3}</math>
 
  
 
== Solution ==
 
== Solution ==
−
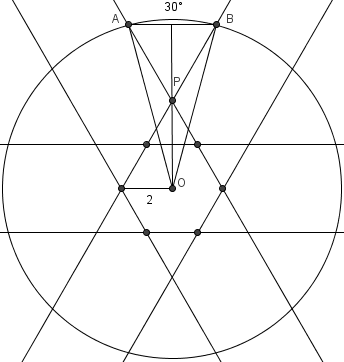
Project any two non-adjacent and non-opposite sides of the [[hexagon]] to the [[circle]]; the [[arc]] between these two points is the locations where all three sides of the hexagon can be fully viewed. Since there are six such pairs of sides, there are six arcs. The probability of choosing a point is <math>1 / 2</math>, or if the total arc degree measures add up to <math>\frac{1}{2} * 360\deg = 180^o</math>. Divide that by six, and each arc must equal <math>30^\mathrm{o}</math>.
+
Project any two non-adjacent and non-opposite sides of the [[hexagon]] to the [[circle]]; the [[arc]] between the two points formed is the location where all three sides of the hexagon can be fully viewed. Since there are six such pairs of sides, there are six arcs. The probability of choosing a point is <math>1 / 2</math>, or if the total arc degree measures add up to <math>\frac{1}{2} \cdot 360^{\circ} = 180^{\circ}</math>. Each arc must equal <math>\frac{180^{\circ}}{6} = 30^\mathrm{\circ}</math>.
−
 
 
−
Call the center <math>O</math>, and the two endpoints of the arc <math>A</math> and <math>B</math>. Angle AOB is equal to the central arc, so it is also 30 degrees. If we extend a line from the center to the midpoint between AB, and we project one of the sides of the hexagon to A and/or B, an [[isosceles triangle]] AXO is formed, with X being the intersection of the extension to the midpoint of AB and the extended side of the hexagon. It is isosceles because angle AOX is 15 degrees, and <math>OAX = OAB - 60 = \frac{180-30}{2} - 60 = 15</math>.
 
−
 
 
−
If we create the perpendicular bisector of AXO from X, then we get a right triangle:
 
−
:<math>\cos 15 = \frac{\frac{r}{2}}{2\sqrt{3}} = \frac{r}{4\sqrt{3}}</math>
 
  
−
Since <math>\cos 15 = \cos (45 - 30) = \frac{\sqrt{6} + \sqrt{2}}{4}</math>, we get:
+
[[Image:2006_12A_AMC-22.png]]
  
−
:<math>\frac{\sqrt{6} + \sqrt{2}}{4} 4\sqrt{3} = r </math>
+
Call the center <math>O</math>, and the two endpoints of the arc <math>A</math> and <math>B</math>, so <math>\angle AOB = 30^{\circ}</math>. Let <math>P</math> be the intersections of the projections of the sides of the hexagon corresponding to <math>\overline{AB}</math>. Notice that <math>\triangle APO</math> is an [[isosceles triangle]]: <math>\angle AOP = 15^{\circ}</math> and <math>\angle OAP = OAB - 60^{\circ} = \frac{180^{\circ}-30^{\circ}}{2} - 60^{\circ} = 15^{\circ}</math>. Since <math>OA</math> is a radius and <math>OP</math> can be found in terms of a side of the hexagon, we are almost done.
  
−
:<math>r = 3\sqrt{2} + \sqrt{6} \Rightarrow \mathrm{D}</math>
+
If we draw the altitude of <math>APO</math> from <math>P</math>, then we get a [[right triangle]]. Using simple trigonometry, <math>\cos 15^{\circ} = \frac{\frac{r}{2}}{2\sqrt{3}} = \frac{r}{4\sqrt{3}}</math>.
  
−
== See also ==
+
Since <math>\cos 15^{\circ} = \cos (45^{\circ} - 30^{\circ}) = \frac{\sqrt{6} + \sqrt{2}}{4}</math>, we get <math>r = \left(\frac{\sqrt{6} + \sqrt{2}}{4}\right) \cdot 4\sqrt{3} = 3\sqrt{2} + \sqrt{6} \Rightarrow \boxed{D}</math>.
−
* [[2006 AMC 12A Problems]]
 
  
 +
== See Also ==
 
{{AMC12 box|year=2006|ab=A|num-b=21|num-a=23}}
 
{{AMC12 box|year=2006|ab=A|num-b=21|num-a=23}}
 +
{{MAA Notice}}
  
 
[[Category:Intermediate Geometry Problems]]
 
[[Category:Intermediate Geometry Problems]]

Latest revision as of 14:39, 14 June 2023

Problem

A circle of radius $r$ is concentric with and outside a regular hexagon of side length $2$. The probability that three entire sides of hexagon are visible from a randomly chosen point on the circle is $1/2$. What is $r$?

$\mathrm{(A) \ } 2\sqrt{2}+2\sqrt{3}\qquad \mathrm{(B) \ } 3\sqrt{3}+\sqrt{2}\qquad \mathrm{(C) \ } 2\sqrt{6}+\sqrt{3}\qquad \rm{(D) \ } 3\sqrt{2}+\sqrt{6}\qquad \mathrm{(E) \ } 6\sqrt{2}-\sqrt{3}$

Solution

Project any two non-adjacent and non-opposite sides of the hexagon to the circle; the arc between the two points formed is the location where all three sides of the hexagon can be fully viewed. Since there are six such pairs of sides, there are six arcs. The probability of choosing a point is $1 / 2$, or if the total arc degree measures add up to $\frac{1}{2} \cdot 360^{\circ} = 180^{\circ}$. Each arc must equal $\frac{180^{\circ}}{6} = 30^\mathrm{\circ}$.

2006 12A AMC-22.png

Call the center $O$, and the two endpoints of the arc $A$ and $B$, so $\angle AOB = 30^{\circ}$. Let $P$ be the intersections of the projections of the sides of the hexagon corresponding to $\overline{AB}$. Notice that $\triangle APO$ is an isosceles triangle: $\angle AOP = 15^{\circ}$ and $\angle OAP = OAB - 60^{\circ} = \frac{180^{\circ}-30^{\circ}}{2} - 60^{\circ} = 15^{\circ}$. Since $OA$ is a radius and $OP$ can be found in terms of a side of the hexagon, we are almost done.

If we draw the altitude of $APO$ from $P$, then we get a right triangle. Using simple trigonometry, $\cos 15^{\circ} = \frac{\frac{r}{2}}{2\sqrt{3}} = \frac{r}{4\sqrt{3}}$.

Since $\cos 15^{\circ} = \cos (45^{\circ} - 30^{\circ}) = \frac{\sqrt{6} + \sqrt{2}}{4}$, we get $r = \left(\frac{\sqrt{6} + \sqrt{2}}{4}\right) \cdot 4\sqrt{3} = 3\sqrt{2} + \sqrt{6} \Rightarrow \boxed{D}$.

See Also

2006 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 21 		Followed by
Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_AMC_12A_Problems/Problem_22&oldid=194392"