Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2006 Cyprus MO/Lyceum/Problem 14"
(solution with note)
 
(4 intermediate revisions by 2 users not shown)
Line 1: Line 1:
 
==Problem==
 
==Problem==
−
<div style="float:right">
+
[[Image:2006 CyMO-14.PNG|250px|right]]
−
[[Image:2006 CyMO-14.PNG|250px]]
 
−
</div>
 
  
−
The rectangle <math>ABCD</math> is a small garden divided to the rectangle <math>AXED</math> and to the square <math>ZBCE</math>, so that <math>AE=2\sqrt{5}m</math> and the shaded area of the triangle <math>DBE</math> is <math>4m^2</math>. The area of the whole garden is
+
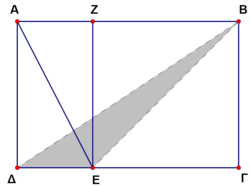
The rectangle <math>AB\Gamma \Delta</math> is a small garden divided to the rectangle <math>AZE\Delta</math> and to the square <math>ZB\Gamma E</math>, so that <math>AE=2\sqrt{5}\ \text{m}</math> and the shaded area of the triangle <math>\Delta BE</math> is <math>4\ \text{m}^2</math>. The area of the whole garden is
  
−
A. <math>24m^2</math>
+
<math>\mathrm{(A)}\ 24\ \text{m}^2\qquad\mathrm{(B)}\ 20\ \text{m}^2\qquad\mathrm{(C)}\ 16\ \text{m}^2\qquad\mathrm{(D)}\ 32\ \text{m}^2\qquad\mathrm{(E)}\ 10\sqrt{5}\ \text{m}^2</math>
  
−
B. <math>20m^2</math>
+
==Solution==
−
 
+
The area of triangle <math>\Delta BE</math> is equal to the area of triangle <math>\Delta AE</math>, so the area of rectangle <math>\Delta AZE</math> is <math>4*2=8</math>. Let <math>AZ=x</math> and <math>XE=y</math>. <math>xy=8</math>, and <math>x^2+y^2=20</math>. Thus
−
C. <math>16m^2</math>
 
−
 
 
−
D. <math>32m^2</math>
 
  
−
E. <math>10\sqrt5m^2</math>
+
<math>(x+y)^2=x^2+y^2+2xy=36\Rightarrow x+y=6</math>. Thus <math>x=2</math> and <math>y=4</math>. So we have <math>[A\Delta \Gamma B]=8+4^2=24\Rightarrow \mathrm{(A)}</math>.
  
−
==Solution==
+
''Note: The answer theoretically can be 12, since we are not given that <math>AZ<ZE</math>. If <math>AZ=4</math> and <math>ZE=2</math>, we have a 2*2 square and a 4*2 rectangle, with a diagonal of <math>2\sqrt{5}</math>. But 12 is not one of the answers included.''
−
{{solution}}
 
  
 
==See also==
 
==See also==
 
{{CYMO box|year=2006|l=Lyceum|num-b=13|num-a=15}}
 
{{CYMO box|year=2006|l=Lyceum|num-b=13|num-a=15}}

Latest revision as of 08:11, 12 August 2008

Problem

2006 CyMO-14.PNG

The rectangle $AB\Gamma \Delta$ is a small garden divided to the rectangle $AZE\Delta$ and to the square $ZB\Gamma E$, so that $AE=2\sqrt{5}\ \text{m}$ and the shaded area of the triangle $\Delta BE$ is $4\ \text{m}^2$. The area of the whole garden is

$\mathrm{(A)}\ 24\ \text{m}^2\qquad\mathrm{(B)}\ 20\ \text{m}^2\qquad\mathrm{(C)}\ 16\ \text{m}^2\qquad\mathrm{(D)}\ 32\ \text{m}^2\qquad\mathrm{(E)}\ 10\sqrt{5}\ \text{m}^2$

Solution

The area of triangle $\Delta BE$ is equal to the area of triangle $\Delta AE$, so the area of rectangle $\Delta AZE$ is $4*2=8$. Let $AZ=x$ and $XE=y$. $xy=8$, and $x^2+y^2=20$. Thus

$(x+y)^2=x^2+y^2+2xy=36\Rightarrow x+y=6$. Thus $x=2$ and $y=4$. So we have $[A\Delta \Gamma B]=8+4^2=24\Rightarrow \mathrm{(A)}$.

Note: The answer theoretically can be 12, since we are not given that $AZ<ZE$. If $AZ=4$ and $ZE=2$, we have a 2*2 square and a 4*2 rectangle, with a diagonal of $2\sqrt{5}$. But 12 is not one of the answers included.

See also

2006 Cyprus MO, Lyceum (Problems)
Preceded by
Problem 13 		Followed by
Problem 15
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_Cyprus_MO/Lyceum/Problem_14&oldid=27379"