Difference between revisions of "2022 AMC 10A Problems/Problem 21"
(→Solution 3 (Not Rigorous)) |
|||
| (35 intermediate revisions by 8 users not shown) | |||
| Line 157: | Line 157: | ||
label("$1$",(r/2,0),S); | label("$1$",(r/2,0),S); | ||
</asy> | </asy> | ||
| − | The area of the octagon is <cmath>3^2-4\cdot\left(\frac12\cdot1 | + | The area of the octagon is <cmath>3^2-4\cdot\left(\frac12\cdot1^2\right)=\boxed{\textbf{(B) }7}.</cmath> |
~MRENTHUSIASM | ~MRENTHUSIASM | ||
| − | ==Solution 2== | + | ==Solution 2 (Symmetry and Similarity) == |
| − | Note that the octagon is equiangular by symmetry, but it is not equilateral. <math>4</math> of | + | (This is an alternate way of analyzing the red extension line segments drawn in Solution 1.) |
| + | |||
| + | The perimeter of the square bottom of the bowl is <math>4</math>. | ||
| + | Halfway up the bowl, the boundary is still a square, with perimeter <math>4</math> times the hexagon circumradius, aka <math>4 \times 2 = 8</math> times the hexagon (also square) side length (1), an increase of <math>4</math>. | ||
| + | |||
| + | Extending the bottom half of the bowl to twice its height (full height of the bowl) would increase the perimeter by the same amount again, forming a square with perimeter <math>4 + (8-4)\times 2= 12</math>. Thus the top octagon is cut out of a square of side length <math>12\div4=3</math> and thus area <math>9</math>. | ||
| + | |||
| + | The difference between the above-constructed square and the octagon is four right triangles, and (by rotational and reflection symmetry), each is isosceles with equal-length perpendicular bases of length <math>(3-1)/2 = 1</math>, and thus having area <math>\frac12</math>. Therefore the area of the octagon is <math>9-(4\times 1/2) = \boxed{\textbf{(B) }7}</math>. | ||
| + | |||
| + | -oinava | ||
| + | |||
| + | ==Solution 3== | ||
| + | |||
| + | Note that the octagon is equiangular by symmetry, but it is not equilateral. <math>4</math> of its sides are shared with the hexagon's sides, so each of those sides have side length <math>1</math>. However, the other <math>4</math> sides are touching the triangles, so we wish to find the length of these sides. | ||
Notice that when two adjacent hexagons meet at a side, their planes make the same dihedral angle at the bottom-most point of intersection and at the top-most point of intersection by symmetry. Therefore, the triangle that is wedged between the two hexagons has the same angle as the square at the bottom wedged between the hexagons. Thus, the triangle is a <math>45-45-90</math> isosceles triangle. | Notice that when two adjacent hexagons meet at a side, their planes make the same dihedral angle at the bottom-most point of intersection and at the top-most point of intersection by symmetry. Therefore, the triangle that is wedged between the two hexagons has the same angle as the square at the bottom wedged between the hexagons. Thus, the triangle is a <math>45-45-90</math> isosceles triangle. | ||
This conclusion can also be reached by cutting the bottom square across a diagonal and noticing that each resulting triangle is congruent to each triangle wedged between the hexagons by symmetry. | This conclusion can also be reached by cutting the bottom square across a diagonal and noticing that each resulting triangle is congruent to each triangle wedged between the hexagons by symmetry. | ||
| − | Furthermore, notice that if you take a copy of this bowl and invert it and place it on top of this bowl, you will get a polyhedron with faces of hexagons and squares, a truncated octahedron, and therefore this triangle has a 90 | + | Furthermore, notice that if you take a copy of this bowl and invert it and place it on top of this bowl, you will get a polyhedron with faces of hexagons and squares, a truncated octahedron, and therefore this triangle has a <math>90^\circ</math>-angle: |
[[File:Screenshot 20221112 010724.png|400px|center]] | [[File:Screenshot 20221112 010724.png|400px|center]] | ||
| Line 174: | Line 187: | ||
We can draw a square around the octagon so that the area of the octagon is the area of the square minus each corner triangle. The hypotenuse of these corner triangles are <math>1</math> and they are <math>45-45-90</math> triangles because the octagon is equiangular, so each has dimensions <math>\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2},1</math>. | We can draw a square around the octagon so that the area of the octagon is the area of the square minus each corner triangle. The hypotenuse of these corner triangles are <math>1</math> and they are <math>45-45-90</math> triangles because the octagon is equiangular, so each has dimensions <math>\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2},1</math>. | ||
| − | The side length of the square is <math>\sqrt{2}</math> for the larger sides of the octagon, and adding 2 of <math>\frac{\sqrt{2}}{2}</math> for each width of the triangle. Therefore, the area of the square is: | + | The side length of the square is <math>\sqrt{2}</math> for the larger sides of the octagon, and adding <math>2</math> of <math>\frac{\sqrt{2}}{2}</math> for each width of the triangle. Therefore, the area of the square is: |
| − | <cmath>\left(\sqrt{2} + 2 \cdot \frac{\sqrt{2}}{2}\right)^2 \implies (2\sqrt{2})^2 = 8</cmath> | + | <cmath>\left(\sqrt{2} + 2 \cdot \frac{\sqrt{2}}{2}\right)^2 \implies \left(2\sqrt{2}\right)^2 = 8</cmath> |
| − | The area of each triangle is <math>\frac{1}{2} \cdot \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{2}}{2} = \frac{1}{4}</math> and there are <math>4</math> of them, so we subtract <math>1</math> from the area of the square. The area of the octagon is thus <math> | + | The area of each triangle is <math>\frac{1}{2} \cdot \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{2}}{2} = \frac{1}{4}</math> and there are <math>4</math> of them, so we subtract <math>1</math> from the area of the square. The area of the octagon is thus <math>\boxed{\textbf{(B) }7}</math>. |
~KingRavi | ~KingRavi | ||
| − | ==Solution 3 (Not Rigorous)== | + | ==Solution 4 (Simple)== |
| + | [[File:2022 AMC 10A 21.png|300px|right]] | ||
| + | [[File:2022 AMC 10A 21b.png|300px|right]] | ||
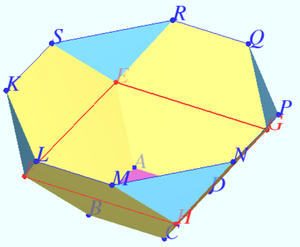
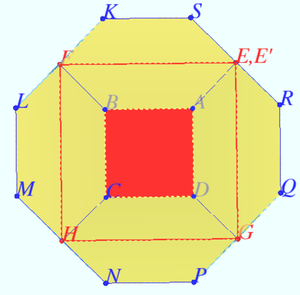
| + | Denote a square <math>ABCD, AB = 1,\pi</math> is the plane <math>ABC,</math> regular hexagons <math>ABFKSE, BCHMLF, CDGPNH, ADGQRE,</math> triangles <math>FKL, ESR, GPQ, HMN.</math> | ||
| + | |||
| + | The main diagonal of each regular hexagon <math>EF = 2 \implies EFGH</math> is square with side <math>2</math> parallel to <math>\pi.</math> | ||
| + | |||
| + | The area of this square <math>[EFGH] = 4 \implies [EFGH] - [ABCD] = 3.</math> | ||
| + | |||
| + | The difference <math>3</math> is the area of the projection of <math>4</math> half of hexagons on the plane <math>\pi.</math> | ||
| + | |||
| + | So the area of the projections of another <math>4</math> half of hexagons is <math>3.</math> | ||
| + | |||
| + | It is evident (may be not only for me) that projections of the coincide sides of hexagons are along diagonals of <math>ABCD</math> (for example <math>A, E, C,</math> and <math>H</math> are collinear.) | ||
| + | |||
| + | So the projections on <math>\pi</math> of the coincide sides of hexagons and triangles are perpendicular to this lines <math>(SE \perp AE).</math> | ||
| + | |||
| + | Therefore in plane <math>\pi</math> projections of points <math>S, E,</math> and <math>R</math> are collinear and plane of <math>\triangle ESR</math> is perpendicular to <math>\pi.</math> | ||
| + | |||
| + | We get <math>1 +3 +3 = \boxed{\textbf{(B) }7}.</math> | ||
| + | |||
| + | PS. Denote <math>A = \left (0.5,0.5, 0 \right), E = \left (1,1, h \right ), E'</math> is the midpoint of <math>RS.</math> | ||
| + | <cmath>|AE| = 1 \implies h = \frac {1}{\sqrt{2}}.</cmath> | ||
| + | <cmath>R = \left( 0.5, 1.5, 2h \right), S = \left (1.5, 0.5, 2h \right) \implies E' = \left( 1, 1, 2h \right) \implies EE' \perp ABC.</cmath> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Solution 5 (Not Rigorous) == | ||
Through observation, we can reasonably assume that each of the triangles on this shape is a right triangle. Since each side length of the hexagons is <math>1</math>, the hypotenuse of the triangles would be <math>\sqrt2</math>. Now we know the side lengths of the octagon whose area we are solving for. The octagon can be broken into nine pieces. We have four triangles whose side lengths are 1, and their hypotenuse is a side whose length is <math>\sqrt2</math>. Next, we have <math>5</math> <math>1</math> by <math>1</math> squares. The triangles each have an area of <math>\frac{1}{2}</math>, and the squares each have an area of <math>1</math>. | Through observation, we can reasonably assume that each of the triangles on this shape is a right triangle. Since each side length of the hexagons is <math>1</math>, the hypotenuse of the triangles would be <math>\sqrt2</math>. Now we know the side lengths of the octagon whose area we are solving for. The octagon can be broken into nine pieces. We have four triangles whose side lengths are 1, and their hypotenuse is a side whose length is <math>\sqrt2</math>. Next, we have <math>5</math> <math>1</math> by <math>1</math> squares. The triangles each have an area of <math>\frac{1}{2}</math>, and the squares each have an area of <math>1</math>. | ||
| Line 186: | Line 226: | ||
~[[OrenSH|orenbad]] | ~[[OrenSH|orenbad]] | ||
| + | |||
| + | ==Solution 6 (Coordinates)== | ||
| + | Let one of the bottom points of the solid be the origin, <math>(0, 0, 0).</math> Then, we can define one of the points where the vertices of the hexagons meet closest to our origin as <math>(x, y, x).</math> Then, note that either the <math>x</math> coordinate or <math>z</math> coordinate must be <math>0</math> in the two vertices closest to the origin in the octagon. We can then let two adjacent points on the octagon near <math>(x, y, x)</math> be <math>(2x, 2y, 0)</math> and <math>(0, 2y, 2x).</math> Since these two points must be a distance of <math>\sqrt{3}</math> from our origin (the height of a regular hexagon), and <math>(x, y, x)</math> must be a distance of <math>1</math> from our origin, we get | ||
| + | <cmath>2x^2+y^2=1, 4x^2+4y^2=3,</cmath> | ||
| + | <cmath>2x^2+y^2=1, x^2+y^2=\frac 34,</cmath> | ||
| + | <cmath>x^2=\frac 14, y^2=\frac 12,</cmath> | ||
| + | <cmath>x=\frac 12, y=\frac{\sqrt 2}{2}.</cmath> | ||
| + | Then, the distance between <math>(2x, 2y, 0)</math> and <math>(0, 2y, 2x)</math> is <math>2\sqrt2 x=\sqrt 2,</math> so the octagon has sides <math>1, \sqrt2, 1, \sqrt2, 1, \sqrt2, 1, \sqrt2,</math> and the solution follows. | ||
| + | |||
| + | -piemax | ||
| + | |||
| + | ==Solution 7 (Parallelogram)== | ||
| + | <asy> | ||
| + | import three; | ||
| + | size(225); | ||
| + | currentprojection= | ||
| + | orthographic(camera=(-5.52541796301147,-2.61548797564715,1.6545450372312), | ||
| + | up=(0.00247902062334861,0.000877141782387748,0.00966536329192992), | ||
| + | target=(0,0,0), | ||
| + | zoom=0.570588560870951); | ||
| + | currentpen = black+1.5bp; | ||
| + | triple A = O; | ||
| + | triple M = (X+Y)/2; | ||
| + | triple B = (-1/2,-1/2,1/sqrt(2)); | ||
| + | triple C = (-1,0,sqrt(2)); | ||
| + | triple D = (0,-1,sqrt(2)); | ||
| + | transform3 rho = rotate(90,M,M+Z); | ||
| + | |||
| + | //arrays of vertices for the lower level (the square), the middle level, | ||
| + | //and the interleaves vertices of the upper level (the octagon) | ||
| + | triple[] lVs = {A}; | ||
| + | triple[] mVs = {B}; | ||
| + | triple[] uVsl = {C}; | ||
| + | triple[] uVsr = {D}; | ||
| + | |||
| + | for(int i = 0; i < 3; ++i){ | ||
| + | lVs.push(rho*lVs[i]); | ||
| + | mVs.push(rho*mVs[i]); | ||
| + | uVsl.push(rho*uVsl[i]); | ||
| + | uVsr.push(rho*uVsr[i]); | ||
| + | } | ||
| + | |||
| + | lVs.cyclic = true; | ||
| + | uVsl.cyclic = true; | ||
| + | |||
| + | for(int i : new int[] {0,1,2,3}){ | ||
| + | draw(uVsl[i]--uVsr[i]); | ||
| + | draw(uVsr[i]--uVsl[i+1]); | ||
| + | } | ||
| + | draw(lVs[0]--lVs[1]^^lVs[0]--lVs[3]); | ||
| + | for(int i : new int[] {0,1,3}){ | ||
| + | draw(lVs[0]--lVs[i]); | ||
| + | draw(lVs[i]--mVs[i]); | ||
| + | draw(mVs[i]--uVsl[i]); | ||
| + | } | ||
| + | for(int i : new int[] {0,3}){ | ||
| + | draw(mVs[i]--uVsr[i]); | ||
| + | } | ||
| + | |||
| + | for(int i : new int[] {1,3}) draw(lVs[2]--lVs[i],dashed); | ||
| + | draw(lVs[2]--mVs[2],dashed); | ||
| + | draw(mVs[2]--uVsl[2]^^mVs[2]--uVsr[2],dashed); | ||
| + | draw(mVs[1]--uVsr[1],dashed); | ||
| + | |||
| + | //Comment two lines below to remove red edges | ||
| + | draw(lVs[1]--lVs[3],red+2bp+dashed); | ||
| + | draw(uVsl[2]--uVsr[2],red+2bp); | ||
| + | draw(uVsl[2]--lVs[1],red+2bp+dashed); | ||
| + | draw(uVsr[2]--lVs[3],red+2bp+dashed); | ||
| + | label("$A$", lVs[3], SW); | ||
| + | label("$B$", lVs[1], SE); | ||
| + | label("$C$", uVsl[2], NE); | ||
| + | label("$D$", uVsr[2], NW); | ||
| + | label("$P$", lVs[2], NE); | ||
| + | label("$Q$", mVs[2], N); | ||
| + | </asy> | ||
| + | |||
| + | Notice that <math>AD \parallel PQ</math>, <math>BC \parallel PQ</math>, so <math>AD \parallel BC</math>. Obviously, <math>AD = BC</math>, so <math>ABCD</math> is a parallelogram, we get <cmath>CD = AB = \sqrt{1^2+1^2} = \sqrt{2}.</cmath> | ||
| + | |||
| + | Note that octagon has four pairs of parallel sides, and the successive side-lengths are <math>1,\sqrt2,1,\sqrt2,1,\sqrt2,1,\sqrt2,</math> as shown below: | ||
| + | <asy> | ||
| + | size(225); | ||
| + | real r = 1/3; | ||
| + | draw((r,0)--(1-r,0)--(1,r)--(1,1-r)--(1-r,1)--(r,1)--(0,1-r)--(0,r)--cycle,black+2bp); | ||
| + | draw((r,0)--(r,1)^^(1-r,0)--(1-r,1)^^(0,r)--(1,r)^^(0,1-r)--(1,1-r), dashed); | ||
| + | label("$1$",(0.5,0),S); | ||
| + | label("$1$",(1,0.5),E); | ||
| + | label("$1$",(0.5,1),N); | ||
| + | label("$1$",(0,0.5),W); | ||
| + | label("$\sqrt2$",(1-r/2,r/2),SE); | ||
| + | label("$\sqrt2$",(1-r/2,1-r/2),NE); | ||
| + | label("$\sqrt2$",(r/2,1-r/2),NW); | ||
| + | label("$\sqrt2$",(r/2,r/2),SW); | ||
| + | label("$1$",(r/2,1/2)); | ||
| + | label("$1$",(1-r/2,1/2)); | ||
| + | label("$1$",(1/2,1/2)); | ||
| + | label("$1$",(1/2,r/2)); | ||
| + | label("$1$",(1/2,1-r/2)); | ||
| + | real rr=r*2/3; | ||
| + | label("$\frac{1}{2}$",(rr,rr)); | ||
| + | label("$\frac{1}{2}$",(1-rr,1-rr)); | ||
| + | label("$\frac{1}{2}$",(rr,1-rr)); | ||
| + | label("$\frac{1}{2}$",(1-rr,rr)); | ||
| + | label("$C$",(r,1),N); | ||
| + | label("$D$",(0,1-r),W); | ||
| + | </asy> | ||
| + | The area of the octagon is <math>\boxed{\textbf{(B) }7}.</math> | ||
| + | |||
| + | ~[https://artofproblemsolving.com/wiki/index.php/User:Reda_mandymath reda_mandymath] | ||
| + | |||
| + | == Animated Video Solution == | ||
| + | https://youtu.be/yk4euPCYhd0 | ||
| + | |||
| + | ~Star League (https://starleague.us) | ||
== Video Solution By ThePuzzlr == | == Video Solution By ThePuzzlr == | ||
| Line 192: | Line 346: | ||
~ MathIsChess | ~ MathIsChess | ||
| − | ==Video Solution by OmegaLearn | + | ==Video Solution by OmegaLearn (Using Equiangular Hexagon Properties)== |
https://youtu.be/-QHhR2r9HgQ | https://youtu.be/-QHhR2r9HgQ | ||
~ pi_is_3.14 | ~ pi_is_3.14 | ||
| + | |||
| + | == Video Solution by MRENTHUSIASM (English & Chinese) == | ||
| + | |||
| + | https://youtu.be/nxssWgtWl9E | ||
| + | |||
| + | ~MRENTHUSIASM | ||
== See Also == | == See Also == | ||
Latest revision as of 04:53, 2 October 2024
Contents
- 1 Problem
- 2 Solution 1
- 3 Solution 2 (Symmetry and Similarity)
- 4 Solution 3
- 5 Solution 4 (Simple)
- 6 Solution 5 (Not Rigorous)
- 7 Solution 6 (Coordinates)
- 8 Solution 7 (Parallelogram)
- 9 Animated Video Solution
- 10 Video Solution By ThePuzzlr
- 11 Video Solution by OmegaLearn (Using Equiangular Hexagon Properties)
- 12 Video Solution by MRENTHUSIASM (English & Chinese)
- 13 See Also
Problem
A bowl is formed by attaching four regular hexagons of side ![]() to a square of side
to a square of side ![]() . The edges of the adjacent hexagons coincide, as shown in the figure. What is the area of the octagon obtained by joining the top eight vertices of the four hexagons, situated on the rim of the bowl?
. The edges of the adjacent hexagons coincide, as shown in the figure. What is the area of the octagon obtained by joining the top eight vertices of the four hexagons, situated on the rim of the bowl?
![[asy] import three; size(225); currentprojection= orthographic(camera=(-5.52541796301147,-2.61548797564715,1.6545450372312), up=(0.00247902062334861,0.000877141782387748,0.00966536329192992), target=(0,0,0), zoom=0.570588560870951); currentpen = black+1.5bp; triple A = O; triple M = (X+Y)/2; triple B = (-1/2,-1/2,1/sqrt(2)); triple C = (-1,0,sqrt(2)); triple D = (0,-1,sqrt(2)); transform3 rho = rotate(90,M,M+Z); //arrays of vertices for the lower level (the square), the middle level, //and the interleaves vertices of the upper level (the octagon) triple[] lVs = {A}; triple[] mVs = {B}; triple[] uVsl = {C}; triple[] uVsr = {D}; for(int i = 0; i < 3; ++i){ lVs.push(rho*lVs[i]); mVs.push(rho*mVs[i]); uVsl.push(rho*uVsl[i]); uVsr.push(rho*uVsr[i]); } lVs.cyclic = true; uVsl.cyclic = true; for(int i : new int[] {0,1,2,3}){ draw(uVsl[i]--uVsr[i]); draw(uVsr[i]--uVsl[i+1]); } draw(lVs[0]--lVs[1]^^lVs[0]--lVs[3]); for(int i : new int[] {0,1,3}){ draw(lVs[0]--lVs[i]); draw(lVs[i]--mVs[i]); draw(mVs[i]--uVsl[i]); } for(int i : new int[] {0,3}){ draw(mVs[i]--uVsr[i]); } for(int i : new int[] {1,3}) draw(lVs[2]--lVs[i],dashed); draw(lVs[2]--mVs[2],dashed); draw(mVs[2]--uVsl[2]^^mVs[2]--uVsr[2],dashed); draw(mVs[1]--uVsr[1],dashed); //Comment two lines below to remove red edges //draw(lVs[1]--lVs[3],red+2bp); //draw(uVsl[0]--uVsr[0],red+2bp); [/asy]](http://latex.artofproblemsolving.com/d/6/0/d604f3d349df2224a285e329575fddb9ffb746a2.png)
![]()
Solution 1
We extend line segments ![]() and
and ![]() to their point of concurrency, as shown below:
to their point of concurrency, as shown below:
![[asy] /* Made by AoPS; edited by MRENTHUSIASM */ import three; size(225); currentprojection= orthographic(camera=(-5.52541796301147,-2.61548797564715,1.6545450372312), up=(0.00247902062334861,0.000877141782387748,0.00966536329192992), target=(0,0,0), zoom=0.570588560870951); currentpen = black+1.5bp; triple A = O; triple M = (X+Y)/2; triple B = (-1/2,-1/2,1/sqrt(2)); triple C = (-1,0,sqrt(2)); triple D = (0,-1,sqrt(2)); transform3 rho = rotate(90,M,M+Z); //arrays of vertices for the lower level (the square), the middle level, //and the interleaves vertices of the upper level (the octagon) triple[] lVs = {A}; triple[] mVs = {B}; triple[] uVsl = {C}; triple[] uVsr = {D}; for(int i = 0; i < 3; ++i){ lVs.push(rho*lVs[i]); mVs.push(rho*mVs[i]); uVsl.push(rho*uVsl[i]); uVsr.push(rho*uVsr[i]); } lVs.cyclic = true; uVsl.cyclic = true; draw(surface(uVsl[0]--uVsr[0]--uVsl[1]--uVsr[1]--uVsl[2]--uVsr[2]--uVsl[3]--uVsr[3]--cycle),yellow); for(int i : new int[] {0,1,2,3}){ draw(uVsl[i]--uVsr[i]); draw(uVsr[i]--uVsl[i+1]); } draw(lVs[0]--lVs[1]^^lVs[0]--lVs[3]); for(int i : new int[] {0,1,3}){ draw(lVs[0]--lVs[i]); draw(lVs[i]--mVs[i]); draw(mVs[i]--uVsl[i]); } for(int i : new int[] {0,3}){ draw(mVs[i]--uVsr[i]); } for(int i : new int[] {1,3}) draw(lVs[2]--lVs[i],dashed); draw(lVs[2]--mVs[2],dashed); draw(mVs[2]--uVsl[2]^^mVs[2]--uVsr[2],dashed); draw(mVs[1]--uVsr[1],dashed); draw(uVsl[1]--uVsr[0],red+2bp); draw(uVsr[3]--uVsl[4],red+2bp); draw(lVs[0]--mVs[0],red+2bp); draw(uVsr[0]--uVsr[0]+uVsr[0]-uVsl[1],red+dashed+2bp); draw(uVsl[4]--uVsl[4]+uVsl[4]-uVsr[3],red+dashed+2bp); draw(mVs[0]--mVs[0]+mVs[0]-lVs[0],red+dashed+2bp); label("$\ell$",midpoint(lVs[0]--mVs[0]),(1,2,0),red); label("$m$",midpoint(uVsr[3]--uVsl[4]),(1,0,-2),red); label("$n$",midpoint(uVsl[1]--uVsr[0]),(-1,0,-2),red); [/asy]](http://latex.artofproblemsolving.com/5/a/1/5a1d01d7732ab18d30112f3e44a0c414be4e063c.png) We claim that lines
We claim that lines ![]() and
and ![]() are concurrent: In the lateral faces of the bowl, we know that lines
are concurrent: In the lateral faces of the bowl, we know that lines ![]() and
and ![]() must intersect, and lines
must intersect, and lines ![]() and
and ![]() must intersect. In addition, line
must intersect. In addition, line ![]() intersects the top plane of the bowl at exactly one point. Since lines
intersects the top plane of the bowl at exactly one point. Since lines ![]() and
and ![]() are both in the top plane of the bowl, we conclude that lines
are both in the top plane of the bowl, we conclude that lines ![]() and
and ![]() are concurrent.
are concurrent.
In the lateral faces of the bowl, the dashed red line segments create equilateral triangles. So, the dashed red line segments all have length ![]() In the top plane of the bowl, we know that
In the top plane of the bowl, we know that ![]() So, the dashed red line segments create an isosceles triangle with leg-length
So, the dashed red line segments create an isosceles triangle with leg-length ![]()
Note that octagon has four pairs of parallel sides, and the successive side-lengths are ![]() as shown below:
as shown below:
![[asy] /* Made by AoPS; edited by MRENTHUSIASM */ size(225); real r = 1/3; draw((0,r)--(0,0)--(r,0)^^(1-r,0)--(1,0)--(1,r)^^(1,1-r)--(1,1)--(1-r,1)^^(r,1)--(0,1)--(0,1-r),red+2bp+dashed); fill((r,0)--(1-r,0)--(1,r)--(1,1-r)--(1-r,1)--(r,1)--(0,1-r)--(0,r)--cycle,yellow); draw((r,0)--(1-r,0)--(1,r)--(1,1-r)--(1-r,1)--(r,1)--(0,1-r)--(0,r)--cycle,black+2bp); label("$1$",(0.5,0),S); label("$1$",(1,0.5),E); label("$1$",(0.5,1),N); label("$1$",(0,0.5),W); label("$\sqrt2$",(1-r/2,r/2),NW); label("$\sqrt2$",(1-r/2,1-r/2),SW); label("$\sqrt2$",(r/2,1-r/2),SE); label("$\sqrt2$",(r/2,r/2),NE); label("$1$",(1-r/2,0),S); label("$1$",(1,r/2),E); label("$1$",(1,1-r/2),E); label("$1$",(1-r/2,1),N); label("$1$",(r/2,1),N); label("$1$",(0,1-r/2),W); label("$1$",(0,r/2),W); label("$1$",(r/2,0),S); [/asy]](http://latex.artofproblemsolving.com/5/9/7/59799f3b193f3540aa706f30914dd8ae61e8f3dd.png) The area of the octagon is
The area of the octagon is ![]()
~MRENTHUSIASM
Solution 2 (Symmetry and Similarity)
(This is an alternate way of analyzing the red extension line segments drawn in Solution 1.)
The perimeter of the square bottom of the bowl is ![]() .
Halfway up the bowl, the boundary is still a square, with perimeter
.
Halfway up the bowl, the boundary is still a square, with perimeter ![]() times the hexagon circumradius, aka
times the hexagon circumradius, aka ![]() times the hexagon (also square) side length (1), an increase of
times the hexagon (also square) side length (1), an increase of ![]() .
.
Extending the bottom half of the bowl to twice its height (full height of the bowl) would increase the perimeter by the same amount again, forming a square with perimeter ![]() . Thus the top octagon is cut out of a square of side length
. Thus the top octagon is cut out of a square of side length ![]() and thus area
and thus area ![]() .
.
The difference between the above-constructed square and the octagon is four right triangles, and (by rotational and reflection symmetry), each is isosceles with equal-length perpendicular bases of length ![]() , and thus having area
, and thus having area ![]() . Therefore the area of the octagon is
. Therefore the area of the octagon is ![]() .
.
-oinava
Solution 3
Note that the octagon is equiangular by symmetry, but it is not equilateral. ![]() of its sides are shared with the hexagon's sides, so each of those sides have side length
of its sides are shared with the hexagon's sides, so each of those sides have side length ![]() . However, the other
. However, the other ![]() sides are touching the triangles, so we wish to find the length of these sides.
sides are touching the triangles, so we wish to find the length of these sides.
Notice that when two adjacent hexagons meet at a side, their planes make the same dihedral angle at the bottom-most point of intersection and at the top-most point of intersection by symmetry. Therefore, the triangle that is wedged between the two hexagons has the same angle as the square at the bottom wedged between the hexagons. Thus, the triangle is a ![]() isosceles triangle.
This conclusion can also be reached by cutting the bottom square across a diagonal and noticing that each resulting triangle is congruent to each triangle wedged between the hexagons by symmetry.
Furthermore, notice that if you take a copy of this bowl and invert it and place it on top of this bowl, you will get a polyhedron with faces of hexagons and squares, a truncated octahedron, and therefore this triangle has a
isosceles triangle.
This conclusion can also be reached by cutting the bottom square across a diagonal and noticing that each resulting triangle is congruent to each triangle wedged between the hexagons by symmetry.
Furthermore, notice that if you take a copy of this bowl and invert it and place it on top of this bowl, you will get a polyhedron with faces of hexagons and squares, a truncated octahedron, and therefore this triangle has a ![]() -angle:
-angle:
Now that we have come to this conclusion, by simple Pythagorean theorem, we have that the other ![]() sides of the octagon are
sides of the octagon are ![]() .
.
We can draw a square around the octagon so that the area of the octagon is the area of the square minus each corner triangle. The hypotenuse of these corner triangles are ![]() and they are
and they are ![]() triangles because the octagon is equiangular, so each has dimensions
triangles because the octagon is equiangular, so each has dimensions ![]() .
The side length of the square is
.
The side length of the square is ![]() for the larger sides of the octagon, and adding
for the larger sides of the octagon, and adding ![]() of
of ![]() for each width of the triangle. Therefore, the area of the square is:
for each width of the triangle. Therefore, the area of the square is:
![\[\left(\sqrt{2} + 2 \cdot \frac{\sqrt{2}}{2}\right)^2 \implies \left(2\sqrt{2}\right)^2 = 8\]](http://latex.artofproblemsolving.com/4/e/7/4e740148f7a81883bc035982026420f43ded26cc.png) The area of each triangle is
The area of each triangle is ![]() and there are
and there are ![]() of them, so we subtract
of them, so we subtract ![]() from the area of the square. The area of the octagon is thus
from the area of the square. The area of the octagon is thus ![]() .
.
~KingRavi
Solution 4 (Simple)
Denote a square ![]() is the plane
is the plane ![]() regular hexagons
regular hexagons ![]() triangles
triangles ![]()
The main diagonal of each regular hexagon ![]() is square with side
is square with side ![]() parallel to
parallel to ![]()
The area of this square ![]()
The difference ![]() is the area of the projection of
is the area of the projection of ![]() half of hexagons on the plane
half of hexagons on the plane ![]()
So the area of the projections of another ![]() half of hexagons is
half of hexagons is ![]()
It is evident (may be not only for me) that projections of the coincide sides of hexagons are along diagonals of ![]() (for example
(for example ![]() and
and ![]() are collinear.)
are collinear.)
So the projections on ![]() of the coincide sides of hexagons and triangles are perpendicular to this lines
of the coincide sides of hexagons and triangles are perpendicular to this lines ![]()
Therefore in plane ![]() projections of points
projections of points ![]() and
and ![]() are collinear and plane of
are collinear and plane of ![]() is perpendicular to
is perpendicular to ![]()
We get ![]()
PS. Denote ![]() is the midpoint of
is the midpoint of ![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
Solution 5 (Not Rigorous)
Through observation, we can reasonably assume that each of the triangles on this shape is a right triangle. Since each side length of the hexagons is ![]() , the hypotenuse of the triangles would be
, the hypotenuse of the triangles would be ![]() . Now we know the side lengths of the octagon whose area we are solving for. The octagon can be broken into nine pieces. We have four triangles whose side lengths are 1, and their hypotenuse is a side whose length is
. Now we know the side lengths of the octagon whose area we are solving for. The octagon can be broken into nine pieces. We have four triangles whose side lengths are 1, and their hypotenuse is a side whose length is ![]() . Next, we have
. Next, we have ![]()
![]() by
by ![]() squares. The triangles each have an area of
squares. The triangles each have an area of ![]() , and the squares each have an area of
, and the squares each have an area of ![]() .
.
Then, we add these up, so we get ![]()
Solution 6 (Coordinates)
Let one of the bottom points of the solid be the origin, ![]() Then, we can define one of the points where the vertices of the hexagons meet closest to our origin as
Then, we can define one of the points where the vertices of the hexagons meet closest to our origin as ![]() Then, note that either the
Then, note that either the ![]() coordinate or
coordinate or ![]() coordinate must be
coordinate must be ![]() in the two vertices closest to the origin in the octagon. We can then let two adjacent points on the octagon near
in the two vertices closest to the origin in the octagon. We can then let two adjacent points on the octagon near ![]() be
be ![]() and
and ![]() Since these two points must be a distance of
Since these two points must be a distance of ![]() from our origin (the height of a regular hexagon), and
from our origin (the height of a regular hexagon), and ![]() must be a distance of
must be a distance of ![]() from our origin, we get
from our origin, we get
![]()
![]()
![]()
![]() Then, the distance between
Then, the distance between ![]() and
and ![]() is
is ![]() so the octagon has sides
so the octagon has sides ![]() and the solution follows.
and the solution follows.
-piemax
Solution 7 (Parallelogram)
![[asy] import three; size(225); currentprojection= orthographic(camera=(-5.52541796301147,-2.61548797564715,1.6545450372312), up=(0.00247902062334861,0.000877141782387748,0.00966536329192992), target=(0,0,0), zoom=0.570588560870951); currentpen = black+1.5bp; triple A = O; triple M = (X+Y)/2; triple B = (-1/2,-1/2,1/sqrt(2)); triple C = (-1,0,sqrt(2)); triple D = (0,-1,sqrt(2)); transform3 rho = rotate(90,M,M+Z); //arrays of vertices for the lower level (the square), the middle level, //and the interleaves vertices of the upper level (the octagon) triple[] lVs = {A}; triple[] mVs = {B}; triple[] uVsl = {C}; triple[] uVsr = {D}; for(int i = 0; i < 3; ++i){ lVs.push(rho*lVs[i]); mVs.push(rho*mVs[i]); uVsl.push(rho*uVsl[i]); uVsr.push(rho*uVsr[i]); } lVs.cyclic = true; uVsl.cyclic = true; for(int i : new int[] {0,1,2,3}){ draw(uVsl[i]--uVsr[i]); draw(uVsr[i]--uVsl[i+1]); } draw(lVs[0]--lVs[1]^^lVs[0]--lVs[3]); for(int i : new int[] {0,1,3}){ draw(lVs[0]--lVs[i]); draw(lVs[i]--mVs[i]); draw(mVs[i]--uVsl[i]); } for(int i : new int[] {0,3}){ draw(mVs[i]--uVsr[i]); } for(int i : new int[] {1,3}) draw(lVs[2]--lVs[i],dashed); draw(lVs[2]--mVs[2],dashed); draw(mVs[2]--uVsl[2]^^mVs[2]--uVsr[2],dashed); draw(mVs[1]--uVsr[1],dashed); //Comment two lines below to remove red edges draw(lVs[1]--lVs[3],red+2bp+dashed); draw(uVsl[2]--uVsr[2],red+2bp); draw(uVsl[2]--lVs[1],red+2bp+dashed); draw(uVsr[2]--lVs[3],red+2bp+dashed); label("$A$", lVs[3], SW); label("$B$", lVs[1], SE); label("$C$", uVsl[2], NE); label("$D$", uVsr[2], NW); label("$P$", lVs[2], NE); label("$Q$", mVs[2], N); [/asy]](http://latex.artofproblemsolving.com/e/c/3/ec30f7882415bc531654556deb7e425772d6cc74.png)
Notice that ![]() ,
, ![]() , so
, so ![]() . Obviously,
. Obviously, ![]() , so
, so ![]() is a parallelogram, we get
is a parallelogram, we get ![]()
Note that octagon has four pairs of parallel sides, and the successive side-lengths are ![]() as shown below:
as shown below:
![[asy] size(225); real r = 1/3; draw((r,0)--(1-r,0)--(1,r)--(1,1-r)--(1-r,1)--(r,1)--(0,1-r)--(0,r)--cycle,black+2bp); draw((r,0)--(r,1)^^(1-r,0)--(1-r,1)^^(0,r)--(1,r)^^(0,1-r)--(1,1-r), dashed); label("$1$",(0.5,0),S); label("$1$",(1,0.5),E); label("$1$",(0.5,1),N); label("$1$",(0,0.5),W); label("$\sqrt2$",(1-r/2,r/2),SE); label("$\sqrt2$",(1-r/2,1-r/2),NE); label("$\sqrt2$",(r/2,1-r/2),NW); label("$\sqrt2$",(r/2,r/2),SW); label("$1$",(r/2,1/2)); label("$1$",(1-r/2,1/2)); label("$1$",(1/2,1/2)); label("$1$",(1/2,r/2)); label("$1$",(1/2,1-r/2)); real rr=r*2/3; label("$\frac{1}{2}$",(rr,rr)); label("$\frac{1}{2}$",(1-rr,1-rr)); label("$\frac{1}{2}$",(rr,1-rr)); label("$\frac{1}{2}$",(1-rr,rr)); label("$C$",(r,1),N); label("$D$",(0,1-r),W); [/asy]](http://latex.artofproblemsolving.com/6/b/2/6b28dd1b2335c0abf3f1a4ca284ba853f3e1dd57.png) The area of the octagon is
The area of the octagon is ![]()
Animated Video Solution
~Star League (https://starleague.us)
Video Solution By ThePuzzlr
~ MathIsChess
Video Solution by OmegaLearn (Using Equiangular Hexagon Properties)
~ pi_is_3.14
Video Solution by MRENTHUSIASM (English & Chinese)
~MRENTHUSIASM
See Also
| 2022 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 20 |
Followed by Problem 22 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.