Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2022 AIME II Problems/Problem 15"

(→‎Solution 3)
m (→‎Solution 3)
 
(17 intermediate revisions by 5 users not shown)
Line 8: Line 8:
 
circle w1=circle(O1,9),w2=circle(O2,6),o=circle(O1,O2,B);
 
circle w1=circle(O1,9),w2=circle(O2,6),o=circle(O1,O2,B);
 
point A=intersectionpoints(o,w2)[1],D=intersectionpoints(o,w2)[0],C=intersectionpoints(o,w1)[0];
 
point A=intersectionpoints(o,w2)[1],D=intersectionpoints(o,w2)[0],C=intersectionpoints(o,w1)[0];
−
filldraw(A--B--O1--C--D--O2--cycle,0.2*red+white,black);
+
filldraw(A--B--O1--C--D--O2--cycle,0.2*fuchsia+white,black);
 
draw(w1);
 
draw(w1);
 
draw(w2);
 
draw(w2);
Line 34: Line 34:
  
 
==Solution 1==
 
==Solution 1==
−
First observe that <math>AO_2 = O_2D</math> and <math>BO_1 = O_1C</math>. Let points <math>A'</math> and <math>B'</math> be the reflections of <math>A</math> and <math>B</math>, respectively, about the perpendicular bisector of <math>\overline{O_1O_2}</math>. Then quadrilaterals <math>ABO_1O_2</math> and <math>A'B'O_2O_1</math> are congruent, so hexagons <math>ABO_1CDO_2</math> and <math>B'A'O_1CDO_2</math> have the same area. Furthermore, triangles <math>DO_2B'</math> and <math>A'O_1C</math> are congruent, so <math>B'D = A'C</math> and quadrilateral <math>B'A'CD</math> is an isosceles trapezoid.
+
First observe that <math>AO_2 = O_2D</math> and <math>BO_1 = O_1C</math>. Let points <math>A'</math> and <math>B'</math> be the reflections of <math>A</math> and <math>B</math>, respectively, about the perpendicular bisector of <math>\overline{O_1O_2}</math>. Then quadrilaterals <math>ABO_1O_2</math> and <math>B'A'O_2O_1</math> are congruent, so hexagons <math>ABO_1CDO_2</math> and <math>A'B'O_1CDO_2</math> have the same area. Furthermore, triangles <math>DO_2A'</math> and <math>B'O_1C</math> are congruent, so <math>A'D = B'C</math> and quadrilateral <math>A'B'CD</math> is an isosceles trapezoid.
 
<asy>
 
<asy>
 
import olympiad;
 
import olympiad;
 
size(180);
 
size(180);
 
defaultpen(linewidth(0.7));
 
defaultpen(linewidth(0.7));
−
pair Bp = dir(105), Ap = dir(75), O1 = dir(25), C = dir(320), D = dir(220), O2 = dir(175);
+
pair Ap = dir(105), Bp = dir(75), O1 = dir(25), C = dir(320), D = dir(220), O2 = dir(175);
−
draw(unitcircle^^Bp--Ap--O1--C--D--O2--cycle);
+
draw(unitcircle^^Ap--Bp--O1--C--D--O2--cycle);
 +
label("$A'$",Ap,dir(origin--Ap));
 
label("$B'$",Bp,dir(origin--Bp));
 
label("$B'$",Bp,dir(origin--Bp));
−
label("$A'$",Ap,dir(origin--Ap));
 
 
label("$O_1$",O1,dir(origin--O1));
 
label("$O_1$",O1,dir(origin--O1));
 
label("$C$",C,dir(origin--C));
 
label("$C$",C,dir(origin--C));
Line 48: Line 48:
 
label("$O_2$",O2,dir(origin--O2));
 
label("$O_2$",O2,dir(origin--O2));
 
draw(O2--O1,linetype("4 4"));
 
draw(O2--O1,linetype("4 4"));
−
draw(Bp--D^^Ap--C,linetype("2 2"));
+
draw(Ap--D^^Bp--C,linetype("2 2"));
 
</asy>
 
</asy>
−
Next, remark that <math>A'O_1 = DO_2</math>, so quadrilateral <math>A'O_1DO_2</math> is also an isosceles trapezoid; in turn, <math>A'D = O_1O_2 = 15</math>, and similarly <math>B'C = 15</math>. Thus, Ptolmey's theorem on <math>B'A'CD</math> yields <math>B'D\cdot A'C + 2\cdot 16 = 15^2</math>, whence <math>B'D = A'C = \sqrt{193}</math>. Let <math>\alpha = \angle B'A'D</math>. The Law of Cosines on triangle <math>B'A'D</math> yields
+
Next, remark that <math>B'O_1 = DO_2</math>, so quadrilateral <math>B'O_1DO_2</math> is also an isosceles trapezoid; in turn, <math>B'D = O_1O_2 = 15</math>, and similarly <math>A'C = 15</math>. Thus, Ptolmey's theorem on <math>A'B'CD</math> yields <math>A'D\cdot B'C + 2\cdot 16 = 15^2</math>, whence <math>A'D = B'C = \sqrt{193}</math>. Let <math>\alpha = \angle A'B'D</math>. The Law of Cosines on triangle <math>A'B'D</math> yields
−
<cmath>\cos\alpha = \frac{15^2 + 2^2 - (\sqrt{193})^2}{2\cdot 2\cdot 15} = \frac{36}{60} = \frac 35,</cmath> and hence <math>\sin\alpha = \tfrac 45</math>. Thus the distance between bases <math>AB</math> and <math>CD</math> is <math>12</math> (in fact, <math>\triangle B'A'D</math> is a <math>9-12-15</math> triangle with a <math>7-12-\sqrt{193}</math> triangle removed), which implies the area of <math>B'A'CD</math> is <math>\tfrac12\cdot 12\cdot(2+16) = 108</math>.
+
<cmath>\cos\alpha = \frac{15^2 + 2^2 - (\sqrt{193})^2}{2\cdot 2\cdot 15} = \frac{36}{60} = \frac 35,</cmath> and hence <math>\sin\alpha = \tfrac 45</math>. Thus the distance between bases <math>A’B’</math> and <math>CD</math> is <math>12</math> (in fact, <math>\triangle A'B'D</math> is a <math>9-12-15</math> triangle with a <math>7-12-\sqrt{193}</math> triangle removed), which implies the area of <math>A'B'CD</math> is <math>\tfrac12\cdot 12\cdot(2+16) = 108</math>.
  
−
Now let <math>O_1C = O_2B' = r_1</math> and <math>O_2D = O_1A' = r_2</math>; the tangency of circles <math>\omega_1</math> and <math>\omega_2</math> implies <math>r_1 +  r_2 = 15</math>. Furthermore, angles <math>B'O_2D</math> and <math>B'A'D</math> are opposite angles in cyclic quadrilateral <math>A'B'O_2D</math>, which implies the measure of angle <math>B'O_2D</math> is <math>180^\circ - \alpha</math>. Therefore, the Law of Cosines applied to triangle <math>\triangle B'O_2D</math> yields
+
Now let <math>O_1C = O_2A' = r_1</math> and <math>O_2D = O_1B' = r_2</math>; the tangency of circles <math>\omega_1</math> and <math>\omega_2</math> implies <math>r_1 +  r_2 = 15</math>. Furthermore, angles <math>A'O_2D</math> and <math>A'B'D</math> are opposite angles in cyclic quadrilateral <math>B'A'O_2D</math>, which implies the measure of angle <math>A'O_2D</math> is <math>180^\circ - \alpha</math>. Therefore, the Law of Cosines applied to triangle <math>\triangle A'O_2D</math> yields
 
<cmath>\begin{align*}
 
<cmath>\begin{align*}
 
193 &= r_1^2 + r_2^2 - 2r_1r_2(-\tfrac 35) = (r_1^2 + 2r_1r_2 + r_2^2) - \tfrac45r_1r_2\\
 
193 &= r_1^2 + r_2^2 - 2r_1r_2(-\tfrac 35) = (r_1^2 + 2r_1r_2 + r_2^2) - \tfrac45r_1r_2\\
Line 59: Line 59:
 
\end{align*}</cmath>
 
\end{align*}</cmath>
  
−
Thus <math>r_1r_2 = 40</math>, and so the area of triangle <math>B'O_2D</math> is <math>\tfrac12r_1r_2\sin\alpha = 16</math>.
+
Thus <math>r_1r_2 = 40</math>, and so the area of triangle <math>A'O_2D</math> is <math>\tfrac12r_1r_2\sin\alpha = 16</math>.
  
 
Thus, the area of hexagon <math>ABO_{1}CDO_{2}</math> is <math>108 + 2\cdot 16 = \boxed{140}</math>.
 
Thus, the area of hexagon <math>ABO_{1}CDO_{2}</math> is <math>108 + 2\cdot 16 = \boxed{140}</math>.
Line 250: Line 250:
  
 
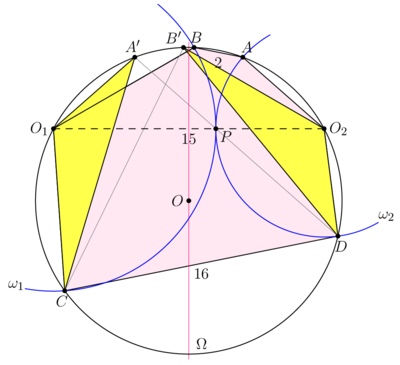
==Solution 3==  
 
==Solution 3==  
−
[[File:AIME 2022 15.png|400px|right]]
+
[[File:AIME-II-2022-15.png|400px|right]]
 
Let points <math>A'</math> and <math>B'</math> be the reflections of <math>A</math> and <math>B,</math> respectively, about the perpendicular bisector of <math>O_1 O_2.</math>  
 
Let points <math>A'</math> and <math>B'</math> be the reflections of <math>A</math> and <math>B,</math> respectively, about the perpendicular bisector of <math>O_1 O_2.</math>  
 
<cmath>B'O_2  = BO_1 = O_1 P = O_1 C,</cmath>
 
<cmath>B'O_2  = BO_1 = O_1 P = O_1 C,</cmath>
Line 259: Line 259:
 
Similarly <math>A'C = B'D \implies \triangle A'CO_1 = \triangle B'DO_2.</math>
 
Similarly <math>A'C = B'D \implies \triangle A'CO_1 = \triangle B'DO_2.</math>
  
−
Ptolmey's theorem on <math>A'CDB'</math> yields <cmath>B'D \cdot A'C + A'B' \cdot CD = A'D \cdot B'C \implies</cmath>
+
Ptolemy's theorem on <math>A'CDB'</math> yields <cmath>B'D \cdot A'C + A'B' \cdot CD = A'D \cdot B'C \implies</cmath>
 
<cmath> B'D^2 + 2 \cdot 16 = 15^2  \implies B'D = A'C = \sqrt{193}.</cmath>
 
<cmath> B'D^2 + 2 \cdot 16 = 15^2  \implies B'D = A'C = \sqrt{193}.</cmath>
 
The area of the trapezoid <math>A'CDB'</math> is equal to the area of an isosceles triangle with sides  
 
The area of the trapezoid <math>A'CDB'</math> is equal to the area of an isosceles triangle with sides  
Line 286: Line 286:
  
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
==Solution 4==
 +
 +
 +
[[File:AIME 2022 II Prob15.jpg|400px|top]]
 +
 +
 +
Let circle <math>O_1</math>'s radius be <math>r</math>, then the radius of circle <math>O_2</math> is <math>15-r</math>. Based on Brahmagupta's Formula,
 +
 +
 +
the hexagon's Area <math>= \sqrt{14(1)(16-r)(1+r)} + \sqrt{7(8)(23-r)(8+r)}</math>.
 +
 +
 +
Now we only need to find the <math>r</math>.
 +
 +
 +
Connect <math>O_1</math> and <math>A</math> , <math>O_1</math> and <math>D</math> , and let  <math>X</math>  be the point of intersection between  <math>O_1D</math>  and  circle <math>O_2</math> , based on the " 2 Non-Congruent Triangles of 'SSA' Scenario " , we can immediately see  <math>O_1X = O_1A</math>  and therefore get an equation from the "Power of A Point Theorem:
 +
 +
 +
<math>(O_1A)(O_1D) = r(15+15-r) = 15r + r(15-r)</math>              (1).
 +
 +
 +
Similarly,
 +
 +
 +
<math>(O_2B)(O_2C) = (15-r)(15+r) = 15(15-r) + r(15-r)</math>      (2).
 +
 +
 +
We can also get two other equations about these 4 segments from Ptolemy's Theorem:
 +
 +
 +
<math>(O_1A)(O_2B) = 30 + r(15-r)</math>              (3)
 +
 +
 +
<math>(O_1D)(O_2C) = 240 + r(15-r)</math>            (4)
 +
 +
 +
Multiply equations (1) and (2), and equations (3) and (4) respectively, we will get a very simple and nice equation of <math>r</math>:
 +
 +
 +
<math>2(15^2)r(15-r) = 7200 + 270r(15-r)</math>,
 +
 +
 +
then:
 +
 +
 +
<math>r(15-r) = 40</math>.
 +
 +
 +
This result is good enough for us to find the hexagon's area, which:
 +
 +
      <math>= \sqrt{14(1)(16-r)(1+r)} + \sqrt{7(8)(23-r)(8+r)}</math>
 +
      <math>= \sqrt{14(1)(1+15-r)(1+r)} + \sqrt{7(8)(8+15-r)(8+r)}</math>
 +
      <math>= \sqrt{14(1)(1+15+40)} + \sqrt{7(8)(64+8(15)+40)}</math>
 +
      <math>= 28 + 112 = \boxed{\textbf{140}}</math>.
 +
 +
eJMaSc
 +
 +
 +
==Video Solution==
 +
https://youtu.be/TeAWS5H5bcc
 +
 +
~MathProblemSolvingSkills.com
 +
  
 
==See Also==
 
==See Also==

Latest revision as of 23:28, 28 June 2023

Problem

Two externally tangent circles $\omega_1$ and $\omega_2$ have centers $O_1$ and $O_2$, respectively. A third circle $\Omega$ passing through $O_1$ and $O_2$ intersects $\omega_1$ at $B$ and $C$ and $\omega_2$ at $A$ and $D$, as shown. Suppose that $AB = 2$, $O_1O_2 = 15$, $CD = 16$, and $ABO_1CDO_2$ is a convex hexagon. Find the area of this hexagon. [asy] import geometry; size(10cm); point O1=(0,0),O2=(15,0),B=9*dir(30); circle w1=circle(O1,9),w2=circle(O2,6),o=circle(O1,O2,B); point A=intersectionpoints(o,w2)[1],D=intersectionpoints(o,w2)[0],C=intersectionpoints(o,w1)[0]; filldraw(A--B--O1--C--D--O2--cycle,0.2*fuchsia+white,black); draw(w1); draw(w2); draw(O1--O2,dashed); draw(o); dot(O1); dot(O2); dot(A); dot(D); dot(C); dot(B); label("$\omega_1$",8*dir(110),SW); label("$\omega_2$",5*dir(70)+(15,0),SE); label("$O_1$",O1,W); label("$O_2$",O2,E); label("$B$",B,N+1/2*E); label("$A$",A,N+1/2*W); label("$C$",C,S+1/4*W); label("$D$",D,S+1/4*E); label("$15$",midpoint(O1--O2),N); label("$16$",midpoint(C--D),N); label("$2$",midpoint(A--B),S); label("$\Omega$",o.C+(o.r-1)*dir(270)); [/asy]

Solution 1

First observe that $AO_2 = O_2D$ and $BO_1 = O_1C$. Let points $A'$ and $B'$ be the reflections of $A$ and $B$, respectively, about the perpendicular bisector of $\overline{O_1O_2}$. Then quadrilaterals $ABO_1O_2$ and $B'A'O_2O_1$ are congruent, so hexagons $ABO_1CDO_2$ and $A'B'O_1CDO_2$ have the same area. Furthermore, triangles $DO_2A'$ and $B'O_1C$ are congruent, so $A'D = B'C$ and quadrilateral $A'B'CD$ is an isosceles trapezoid. [asy] import olympiad; size(180); defaultpen(linewidth(0.7)); pair Ap = dir(105), Bp = dir(75), O1 = dir(25), C = dir(320), D = dir(220), O2 = dir(175); draw(unitcircle^^Ap--Bp--O1--C--D--O2--cycle); label("$A'$",Ap,dir(origin--Ap)); label("$B'$",Bp,dir(origin--Bp)); label("$O_1$",O1,dir(origin--O1)); label("$C$",C,dir(origin--C)); label("$D$",D,dir(origin--D)); label("$O_2$",O2,dir(origin--O2)); draw(O2--O1,linetype("4 4")); draw(Ap--D^^Bp--C,linetype("2 2")); [/asy] Next, remark that $B'O_1 = DO_2$, so quadrilateral $B'O_1DO_2$ is also an isosceles trapezoid; in turn, $B'D = O_1O_2 = 15$, and similarly $A'C = 15$. Thus, Ptolmey's theorem on $A'B'CD$ yields $A'D\cdot B'C + 2\cdot 16 = 15^2$, whence $A'D = B'C = \sqrt{193}$. Let $\alpha = \angle A'B'D$. The Law of Cosines on triangle $A'B'D$ yields \[\cos\alpha = \frac{15^2 + 2^2 - (\sqrt{193})^2}{2\cdot 2\cdot 15} = \frac{36}{60} = \frac 35,\] and hence $\sin\alpha = \tfrac 45$. Thus the distance between bases $A’B’$ and $CD$ is $12$ (in fact, $\triangle A'B'D$ is a $9-12-15$ triangle with a $7-12-\sqrt{193}$ triangle removed), which implies the area of $A'B'CD$ is $\tfrac12\cdot 12\cdot(2+16) = 108$.

Now let $O_1C = O_2A' = r_1$ and $O_2D = O_1B' = r_2$; the tangency of circles $\omega_1$ and $\omega_2$ implies $r_1 + r_2 = 15$. Furthermore, angles $A'O_2D$ and $A'B'D$ are opposite angles in cyclic quadrilateral $B'A'O_2D$, which implies the measure of angle $A'O_2D$ is $180^\circ - \alpha$. Therefore, the Law of Cosines applied to triangle $\triangle A'O_2D$ yields \begin{align*} 193 &= r_1^2 + r_2^2 - 2r_1r_2(-\tfrac 35) = (r_1^2 + 2r_1r_2 + r_2^2) - \tfrac45r_1r_2\\ &= (r_1+r_2)^2 - \tfrac45 r_1r_2 = 225 - \tfrac45r_1r_2. \end{align*}

Thus $r_1r_2 = 40$, and so the area of triangle $A'O_2D$ is $\tfrac12r_1r_2\sin\alpha = 16$.

Thus, the area of hexagon $ABO_{1}CDO_{2}$ is $108 + 2\cdot 16 = \boxed{140}$.

~djmathman

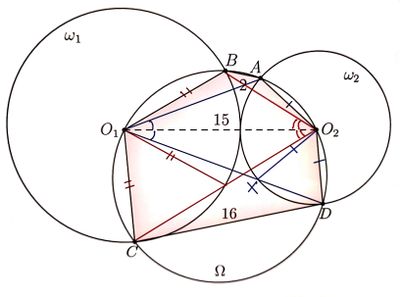
Solution 2

Denote by $O$ the center of $\Omega$. Denote by $r$ the radius of $\Omega$.

We have $O_1$, $O_2$, $A$, $B$, $C$, $D$ are all on circle $\Omega$.

Denote $\angle O_1 O O_2 = 2 \theta$. Denote $\angle O_1 O B = \alpha$. Denote $\angle O_2 O A = \beta$.

Because $B$ and $C$ are on circles $\omega_1$ and $\Omega$, $BC$ is a perpendicular bisector of $O_1 O$. Hence, $\angle O_1 O C = \alpha$.

Because $A$ and $D$ are on circles $\omega_2$ and $\Omega$, $AD$ is a perpendicular bisector of $O_2 O$. Hence, $\angle O_2 O D = \beta$.

In $\triangle O O_1 O_2$, \[ O_1 O_2 = 2 r \sin \theta . \]

Hence, \[ 2 r \sin \theta = 15 . \]

In $\triangle O AB$, \begin{align*} AB & = 2 r \sin \frac{2 \theta - \alpha - \beta}{2} \\ & = 2 r \sin \theta \cos \frac{\alpha + \beta}{2} - 2 r \cos \theta \sin \frac{\alpha + \beta}{2} \\ & = 15 \cos \frac{\alpha + \beta}{2} - 2 r \cos \theta \sin \frac{\alpha + \beta}{2} . \end{align*}

Hence, \[ 15 \cos \frac{\alpha + \beta}{2} - 2 r \cos \theta \sin \frac{\alpha + \beta}{2} = 2 . \hspace{1cm} (1) \]


In $\triangle O CD$, \begin{align*} CD & = 2 r \sin \frac{360^\circ - 2 \theta - \alpha - \beta}{2} \\ & = 2 r \sin \left( \theta + \frac{\alpha + \beta}{2} \right) \\ & = 2 r \sin \theta \cos \frac{\alpha + \beta}{2} + 2 r \cos \theta \sin \frac{\alpha + \beta}{2} \\ & = 15 \cos \frac{\alpha + \beta}{2} + 2 r \cos \theta \sin \frac{\alpha + \beta}{2} . \end{align*}

Hence, \[ 15 \cos \frac{\alpha + \beta}{2} + 2 r \cos \theta \sin \frac{\alpha + \beta}{2} = 16 . \hspace{1cm} (2) \]

Taking $\frac{(1) + (2)}{30}$, we get $\cos \frac{\alpha + \beta}{2} = \frac{3}{5}$. Thus, $\sin \frac{\alpha + \beta}{2} = \frac{4}{5}$.

Taking these into (1), we get $2 r \cos \theta = \frac{35}{4}$. Hence, \begin{align*} 2 r & = \sqrt{ \left( 2 r \sin \theta \right)^2 + \left( 2 r \cos \theta \right)^2} \\ & = \frac{5}{4} \sqrt{193} . \end{align*}

Hence, $\cos \theta = \frac{7}{\sqrt{193}}$.

In $\triangle O O_1 B$, \[ O_1 B = 2 r \sin \frac{\alpha}{2} . \]

In $\triangle O O_2 A$, by applying the law of sines, we get \[ O_2 A = 2 r \sin \frac{\beta}{2} . \]

Because circles $\omega_1$ and $\omega_2$ are externally tangent, $B$ is on circle $\omega_1$, $A$ is on circle $\omega_2$, \begin{align*} O_1 O_2 & = O_1 B + O_2 A \\ & = 2 r \sin \frac{\alpha}{2} + 2 r \sin \frac{\beta}{2} \\ & = 2 r \left( \sin \frac{\alpha}{2} + \sin \frac{\beta}{2} \right) . \end{align*}

Thus, $\sin \frac{\alpha}{2} + \sin \frac{\beta}{2} = \frac{12}{\sqrt{193}}$.

Now, we compute $\sin \alpha$ and $\sin \beta$.

Recall $\cos \frac{\alpha + \beta}{2} = \frac{3}{5}$ and $\sin \frac{\alpha + \beta}{2} = \frac{4}{5}$. Thus, $e^{i \frac{\alpha}{2}} e^{i \frac{\beta}{2}} = e^{i \frac{\alpha + \beta}{2}} = \frac{3}{5} + i \frac{4}{5}$.

We also have \begin{align*} \sin \frac{\alpha}{2} + \sin \frac{\beta}{2} & = \frac{1}{2i} \left( e^{i \frac{\alpha}{2}} - e^{-i \frac{\alpha}{2}} + e^{i \frac{\beta}{2}} - e^{-i \frac{\beta}{2}} \right) \\ & = \frac{1}{2i} \left( 1 - \frac{1}{e^{i \frac{\alpha + \beta}{2}} } \right) \left( e^{i \frac{\alpha}{2}} + e^{i \frac{\beta}{2}} \right) . \end{align*}

Thus, \begin{align*} \sin \alpha + \sin \beta & = \frac{1}{2i} \left( e^{i \alpha} - e^{-i \alpha} + e^{i \beta} - e^{-i \beta} \right) \\ & = \frac{1}{2i} \left( 1 - \frac{1}{e^{i \left( \alpha + \beta \right)}} \right) \left( e^{i \alpha} + e^{i \beta} \right) \\ & = \frac{1}{2i} \left( 1 - \frac{1}{e^{i \left( \alpha + \beta \right)}} \right) \left( \left( e^{i \frac{\alpha}{2}} + e^{i \frac{\beta}{2}} \right)^2 - 2 e^{i \frac{\alpha + \beta}{2}} \right) \\ & = \frac{1}{2i} \left( 1 - \frac{1}{e^{i \left( \alpha + \beta \right)}} \right) \left( \left( \frac{2 i \left( \sin \frac{\alpha}{2} + \sin \frac{\beta}{2} \right)}{1 - \frac{1}{e^{i \frac{\alpha + \beta}{2}} }} \right)^2 - 2 e^{i \frac{\alpha + \beta}{2}} \right) \\ & = - \frac{1}{i} \left( e^{i \frac{\alpha + \beta}{2}} - e^{-i \frac{\alpha + \beta}{2}} \right) \left( \frac{2 \left( \sin \frac{\alpha}{2} + \sin \frac{\beta}{2} \right)^2} {e^{i \frac{\alpha + \beta}{2}} + e^{-i \frac{\alpha + \beta}{2}} - 2 } + 1 \right) \\ & = \frac{167 \cdot 8}{193 \cdot 5 } . \end{align*}

Therefore, \begin{align*} {\rm Area} \ ABO_1CDO_2 & = {\rm Area} \ \triangle O_3 AB + {\rm Area} \ \triangle O_3 BO_1 + {\rm Area} \ \triangle O_3 O_1 C \\ & \quad + {\rm Area} \ \triangle O_3 C D + {\rm Area} \ \triangle O_3 D O_2 + {\rm Area} \ \triangle O_3 O_2 A \\ & = \frac{1}{2} r^2 \left( \sin \left( 2 \theta - \alpha - \beta \right) + \sin \alpha + \sin \alpha + \sin \left( 360^\circ - 2 \theta - \alpha - \beta \right) + \sin \beta + \sin \beta \right) \\ & = \frac{1}{2} r^2 \left( \sin \left( 2 \theta - \alpha - \beta \right) - \sin \left( 2 \theta + \alpha + \beta \right) + 2 \sin \alpha + 2 \sin \beta \right) \\ & = r^2 \left( - \cos 2 \theta \sin \left( \alpha + \beta \right) + \sin \alpha + \sin \beta \right) \\ & = r^2 \left( \left( 1 - 2 \cos^2 \theta \right) 2 \sin \frac{\alpha + \beta}{2} \cos \frac{\alpha + \beta}{2} + \sin \alpha + \sin \beta \right) \\ & = \boxed{\textbf{(140) }} . \end{align*}

~Steven Chen (www.professorchenedu.com)

Solution 3

AIME-II-2022-15.png

Let points $A'$ and $B'$ be the reflections of $A$ and $B,$ respectively, about the perpendicular bisector of $O_1 O_2.$ \[B'O_2 = BO_1 = O_1 P = O_1 C,\] \[A'O_1 = AO_2 = O_2 P = O_2 D.\] We establish the equality of the arcs and conclude that the corresponding chords are equal \[\overset{\Large\frown} {CO_1} + \overset{\Large\frown} {A'O_1} +\overset{\Large\frown} {A'B'} = \overset{\Large\frown} {B'O_2} +\overset{\Large\frown} {A'O_1} +\overset{\Large\frown} {A'B'} =\overset{\Large\frown} {B'O_2} +\overset{\Large\frown} {DO_2} +\overset{\Large\frown} {A'B'}\] \[\implies A'D = B'C = O_1 O_2 = 15.\] Similarly $A'C = B'D \implies \triangle A'CO_1 = \triangle B'DO_2.$

Ptolemy's theorem on $A'CDB'$ yields \[B'D \cdot A'C + A'B' \cdot CD = A'D \cdot B'C \implies\] \[B'D^2 + 2 \cdot 16 = 15^2 \implies B'D = A'C = \sqrt{193}.\] The area of the trapezoid $A'CDB'$ is equal to the area of an isosceles triangle with sides $A'D = B'C = 15$ and $A'B' + CD = 18.$

The height of this triangle is $\sqrt{15^2-9^2} = 12.$ The area of $A'CDB'$ is $108.$

\[\sin \angle B'CD = \frac{12}{15} = \frac{4}{5},\] \[\angle B'CD + \angle B'O_2 D = 180^o \implies \sin \angle B'O_2 D = \frac{4}{5}.\]

Denote $\angle B'O_2 D = 2\alpha.$ $\angle B'O_2 D > \frac{\pi}{2},$ hence $\cos \angle B'O_2 D = \cos 2\alpha = -\frac{3}{5}.$ \[\tan \alpha =\frac { \sin 2 \alpha}{1+\cos 2 \alpha} = \frac {4/5}{1 - 3/5}=2.\]

Semiperimeter of $\triangle B'O_2 D$ is $s = \frac {15 + \sqrt{193}}{2}.$

The distance from the vertex $O_2$ to the tangent points of the inscribed circle of the triangle $B'O_2 D$ is equal $s – B'D = \frac{15 – \sqrt{193}}{2}.$

The radius of the inscribed circle is $r = (s – B'D) \tan \alpha.$

The area of triangle $B'O_2 D$ is $[B'O_2 D] = sr = s (s – B'D) \tan \alpha = \frac {15^2 – 193}{2} = 16.$

The hexagon $ABO_1 CDO_2$ has the same area as hexagon $B'A'O_1 CDO_2.$

The area of hexagon $B'A'O_1 CDO_2$ is equal to the sum of the area of the trapezoid $A'CDB'$ and the areas of two equal triangles $B'O_2 D$ and $A'O_1 C,$ so the area of the hexagon $ABO_1 CDO_2$ is \[108 + 16 + 16 = \boxed{140}.\]

vladimir.shelomovskii@gmail.com, vvsss

Solution 4

AIME 2022 II Prob15.jpg


Let circle $O_1$'s radius be $r$, then the radius of circle $O_2$ is $15-r$. Based on Brahmagupta's Formula,


the hexagon's Area $= \sqrt{14(1)(16-r)(1+r)} + \sqrt{7(8)(23-r)(8+r)}$.


Now we only need to find the $r$.


Connect $O_1$ and $A$ , $O_1$ and $D$ , and let $X$ be the point of intersection between $O_1D$ and circle $O_2$ , based on the " 2 Non-Congruent Triangles of 'SSA' Scenario " , we can immediately see $O_1X = O_1A$ and therefore get an equation from the "Power of A Point Theorem:


$(O_1A)(O_1D) = r(15+15-r) = 15r + r(15-r)$ (1).


Similarly,


$(O_2B)(O_2C) = (15-r)(15+r) = 15(15-r) + r(15-r)$ (2).


We can also get two other equations about these 4 segments from Ptolemy's Theorem:


$(O_1A)(O_2B) = 30 + r(15-r)$ (3)


$(O_1D)(O_2C) = 240 + r(15-r)$ (4)


Multiply equations (1) and (2), and equations (3) and (4) respectively, we will get a very simple and nice equation of $r$:


$2(15^2)r(15-r) = 7200 + 270r(15-r)$,


then:


$r(15-r) = 40$.


This result is good enough for us to find the hexagon's area, which: 

     $= \sqrt{14(1)(16-r)(1+r)} + \sqrt{7(8)(23-r)(8+r)}$
     $= \sqrt{14(1)(1+15-r)(1+r)} + \sqrt{7(8)(8+15-r)(8+r)}$
     $= \sqrt{14(1)(1+15+40)} + \sqrt{7(8)(64+8(15)+40)}$
     $= 28 + 112 = \boxed{\textbf{140}}$.

eJMaSc


Video Solution

https://youtu.be/TeAWS5H5bcc

~MathProblemSolvingSkills.com


See Also

2022 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2022_AIME_II_Problems/Problem_15&oldid=194924"