Difference between revisions of "2005 AMC 10A Problems"

Revision as of 19:46, 30 January 2011

Problem 1

While eating out, Mike and Joe each tipped their server $2$ dollars. Mike tipped $10\%$ of his bill and Joe tipped $20\%$ of his bill. What was the difference, in dollars between their bills?

$\mathrm{(A) \ } 2\qquad \mathrm{(B) \ } 4\qquad \mathrm{(C) \ } 5\qquad \mathrm{(D) \ } 10\qquad \mathrm{(E) \ } 20$

Solution

Problem 2

For each pair of real numbers $a$ $\neq$ $b$ , define the operation $\star$ as

$(a \star b) = \frac{a+b}{a-b}$ .

What is the value of $((1 \star 2) \star 3)$ ?

$\mathrm{(A) \ } -\frac{2}{3}\qquad \mathrm{(B) \ } -\frac{1}{5}\qquad \mathrm{(C) \ } 0\qquad \mathrm{(D) \ } \frac{1}{2}\qquad \mathrm{(E) \ } \textrm{This\, value\, is\, not\, defined.}$

Solution

Problem 3

The equations $2x + 7 = 3$ and $bx - 10 = -2$ have the same solution $x$ . What is the value of $b$ ?

$\mathrm{(A) \ } -8\qquad \mathrm{(B) \ } -4\qquad \mathrm{(C) \ } -2\qquad \mathrm{(D) \ } 4\qquad \mathrm{(E) \ } 8$

Solution

Problem 4

A rectangle with a diagonal of length $x$ is twice as long as it is wide. What is the area of the rectangle?

$\mathrm{(A) \ } \frac{1}{4}x^2\qquad \mathrm{(B) \ } \frac{2}{5}x^2\qquad \mathrm{(C) \ } \frac{1}{2}x^2\qquad \mathrm{(D) \ } x^2\qquad \mathrm{(E) \ } \frac{3}{2}x^2$

Solution

Problem 5

A store normally sells windows at <dollar/>100 each. This week the store is offering one free window for each purchase of four. Dave needs seven windows and Doug needs eight windows. How many dollars will they save if they purchase the windows together rather than separately?

$\mathrm{(A) \ } 100\qquad \mathrm{(B) \ } 200\qquad \mathrm{(C) \ } 300\qquad \mathrm{(D) \ } 400\qquad \mathrm{(E) \ } 500$

Solution

Problem 6

The average (mean) of $20$ numbers is $30$ , and the average of $30$ other numbers is $20$ . What is the average of all $50$ numbers?

$\mathrm{(A) \ } 23\qquad \mathrm{(B) \ } 24\qquad \mathrm{(C) \ } 25\qquad \mathrm{(D) \ } 26\qquad \mathrm{(E) \ } 27$

Solution

Problem 7

Josh and Mike live $13$ miles apart. Yesterday Josh started to ride his bicycle toward Mike's house. A little later Mike started to ride his bicycle toward Josh's house. When they met, Josh had ridden for twice the length of time as Mike and at four-fifths of Mike's rate. How many miles had Mike ridden when they met?

$\mathrm{(A) \ } 4\qquad \mathrm{(B) \ } 5\qquad \mathrm{(C) \ } 6\qquad \mathrm{(D) \ } 7\qquad \mathrm{(E) \ } 8$

Solution

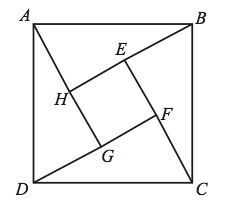
Problem 8

In the figure, the length of side $AB$ of square $ABCD$ is $\sqrt{50}$ and $BE$ =1. What is the area of the inner square $EFGH$ ?

$\textbf{(A)}\ 25\qquad\textbf{(B)}\ 32\qquad\textbf{(C)}\ 36\qquad\textbf{(D)}\ 40\qquad\textbf{(E)}\ 42$

Solution

Problem 9

Three tiles are marked $X$ and two other tiles are marked $O$ . The five tiles are randomly arranged in a row. What is the probability that the arrangement reads $XOXOX$ ?

$\mathrm{(A) \ } \frac{1}{12}\qquad \mathrm{(B) \ } \frac{1}{10}\qquad \mathrm{(C) \ } \frac{1}{6}\qquad \mathrm{(D) \ } \frac{1}{4}\qquad \mathrm{(E) \ } \frac{1}{3}$

Solution

Problem 10

There are two values of $a$ for which the equation $4x^2 + ax + 8x + 9 = 0$ has only one solution for $x$ . What is the sum of those values of $a$ ?

$\mathrm{(A) \ } -16\qquad \mathrm{(B) \ } -8\qquad \mathrm{(C) \ } 0\qquad \mathrm{(D) \ } 8\qquad \mathrm{(E) \ } 20$

Solution

Problem 11

A wooden cube $n$ units on a side is painted red on all six faces and then cut into $n^3$ unit cubes. Exactly one-fourth of the total number of faces of the unit cubes are red. What is $n$ ?

$\mathrm{(A) \ } 3\qquad \mathrm{(B) \ } 4\qquad \mathrm{(C) \ } 5\qquad \mathrm{(D) \ } 6\qquad \mathrm{(E) \ } 7$

Solution

Problem 12

The figure shown is called a trefoil and is constructed by drawing circular sectors about the sides of the congruent equilateral triangles. What is the area of a trefoil whose horizontal base has length $2$ ?

$\mathrm{(A) \ } \frac{1}{3}\pi+\frac{\sqrt{3}}{2}\qquad \mathrm{(B) \ } \frac{2}{3}\pi\qquad \mathrm{(C) \ } \frac{2}{3}\pi+\frac{\sqrt{3}}{4}\qquad \mathrm{(D) \ } \frac{2}{3}\pi+\frac{\sqrt{3}}{3}\qquad \mathrm{(E) \ } \frac{2}{3}\pi+\frac{\sqrt{3}}{2}$

Solution

Problem 13

How many positive integers $n$ satisfy the following condition:

$(130n)^{50} > n^{100} > 2^{200}$ ?

$\mathrm{(A) \ } 0\qquad \mathrm{(B) \ } 7\qquad \mathrm{(C) \ } 12\qquad \mathrm{(D) \ } 65\qquad \mathrm{(E) \ } 125$

Solution

Problem 14

How many three-digit numbers satisfy the property that the middle digit is the average of the first and the last digits?

$\mathrm{(A) \ } 41\qquad \mathrm{(B) \ } 42\qquad \mathrm{(C) \ } 43\qquad \mathrm{(D) \ } 44\qquad \mathrm{(E) \ } 45$

Solution

Problem 15

How many positive cubes divide $3! \cdot 5! \cdot 7!$ ?

$\mathrm{(A) \ } 2\qquad \mathrm{(B) \ } 3\qquad \mathrm{(C) \ } 4\qquad \mathrm{(D) \ } 5\qquad \mathrm{(E) \ } 6$

Solution

Problem 16

The sum of the digits of a two-digit number is subtracted from the number. The units digit of the result is $6$ . How many two-digit numbers have this property?

$\mathrm{(A) \ } 5\qquad \mathrm{(B) \ } 7\qquad \mathrm{(C) \ } 9\qquad \mathrm{(D) \ } 10\qquad \mathrm{(E) \ } 19$

Solution

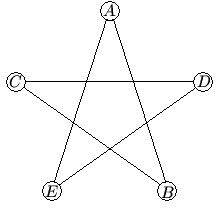
Problem 17

In the five-sided star shown, the letters $A$ , $B$ , $C$ , $D$ , and $E$ are replaced by the numbers $3$ , $5$ , $6$ , $7$ , and $9$ , although not necessarily in this order. The sums of the numbers at the ends of the line segments $AB$ , $BC$ , $CD$ , $DE$ , and $EA$ form an arithmetic sequence, although not necessarily in this order. What is the middle term of the sequence?

$\mathrm{(A) \ } 9\qquad \mathrm{(B) \ } 10\qquad \mathrm{(C) \ } 11\qquad \mathrm{(D) \ } 12\qquad \mathrm{(E) \ } 13$

Solution

Problem 18

Team A and team B play a series. The first team to win three games wins the series. Each team is equally likely to win each game, there are no ties, and the outcomes of the individual games are independent. If team B wins the second game and team A wins the series, what is the probability that team B wins the first game?

$\mathrm{(A) \ } \frac{1}{5}\qquad \mathrm{(B) \ } \frac{1}{4}\qquad \mathrm{(C) \ } \frac{1}{3}\qquad \mathrm{(D) \ } \frac{1}{2}\qquad \mathrm{(E) \ } \frac{2}{3}$

Solution

Problem 19

19 Solution

Problem 20

An equiangular octagon has four sides of length 1 and four sides of length $\frac{\sqrt{2}}{2}$ , arranged so that no two consecutive sides have the same length. What is the area of the octagon?

$\mathrm{(A) \ } \frac72\qquad \mathrm{(B) \ } \frac{7\sqrt2}{2}\qquad \mathrm{(C) \ } \frac{5+4\sqrt2}{2}\qquad \mathrm{(D) \ } \frac{4+5\sqrt2}{2}\qquad \mathrm{(E) \ } 7$

Solution

Problem 21

For how many positive integers $n$ does $1+2+...+n$ evenly divide from $6n$ ?

$\mathrm{(A) \ } 3\qquad \mathrm{(B) \ } 5\qquad \mathrm{(C) \ } 7\qquad \mathrm{(D) \ } 9\qquad \mathrm{(E) \ } 11$

Solution

Problem 22

Let $S$ be the set of the $2005$ smallest positive multiples of $4$ , and let $T$ be the set of the $2005$ smallest positive multiples of $6$ . How many elements are common to $S$ and $T$ ?

$\mathrm{(A) \ } 166\qquad \mathrm{(B) \ } 333\qquad \mathrm{(C) \ } 500\qquad \mathrm{(D) \ } 668\qquad \mathrm{(E) \ } 1001$

Solution

Problem 23

Let $AB$ be a diameter of a circle and let $C$ be a point on $AB$ with $2\cdot AC=BC$ . Let $D$ and $E$ be points on the circle such that $DC \perp AB$ and $DE$ is a second diameter. What is the ratio of the area of $\triangle DCE$ to the area of $\triangle ABD$ ?

$\mathrm{(A) \ } \frac{1}{6} \qquad \mathrm{(B) \ } \frac{1}{4} \qquad \mathrm{(C) \ } \frac{1}{3} \qquad \mathrm{(D) \ } \frac{1}{2} \qquad \mathrm{(E) \ } \frac{2}{3}$

Solution

Problem 24

For each positive integer $m > 1$ , let $P(m)$ denote the greatest prime factor of $m$ . For how many positive integers $n$ is it true that both $P(n) = \sqrt{n}$ and $P(n+48) = \sqrt{n+48}$ ?

$\mathrm{(A) \ } 0\qquad \mathrm{(B) \ } 1\qquad \mathrm{(C) \ } 3\qquad \mathrm{(D) \ } 4\qquad \mathrm{(E) \ } 5$

Solution

Problem 25

In $ABC$ we have $AB = 25$ , $BC = 39$ , and $AC=42$ . Points $D$ and $E$ are on $AB$ and $AC$ respectively, with $AD = 19$ and $AE = 14$ . What is the ratio of the area of triangle $ADE$ to the area of the quadrilateral $BCED$ ?

$\mathrm{(A) \ } \frac{266}{1521}\qquad \mathrm{(B) \ } \frac{19}{75}\qquad \mathrm{(C) \ } \frac{1}{3}\qquad \mathrm{(D) \ } \frac{19}{56}\qquad \mathrm{(E) \ } 1$

Solution

@@ Line 56: / Line 56: @@
 [[File:AMC102005Aq.png]]
+<math> \textbf{(A)}\ 25\qquad\textbf{(B)}\ 32\qquad\textbf{(C)}\ 36\qquad\textbf{(D)}\ 40\qquad\textbf{(E)}\ 42 </math>
 [[2005 AMC 10A Problems/Problem 8|Solution]]

Page

Toolbox

Search

Difference between revisions of "2005 AMC 10A Problems"

Revision as of 19:46, 30 January 2011

Contents

Problem 1

Problem 2

Problem 3

Problem 4

Problem 5

Problem 6

Problem 7

Problem 8

Problem 9

Problem 10

Problem 11

Problem 12

Problem 13

Problem 14

Problem 15

Problem 16

Problem 17

Problem 18

Problem 19

Problem 20

Problem 21

Problem 22

Problem 23

Problem 24

Problem 25

See also