Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2023 AMC 12A Problems/Problem 21"

(→‎Solution 8 (Dodecahedron Schlegel Diagram))
(→‎Solution 8 (Dodecahedron Schlegel Diagram))
Line 126: Line 126:
 
import three;
 
import three;
  
−
// Define the camera view
+
// Definition for drawing pentagon
−
currentprojection = orthographic(0,10,5);
+
void drawPentagon(triple c, triple dir, real size, pen color) {
 +
  real angle = 72;
 +
  triple[] pts;
  
−
// Setting up a function to create a regular pentagon
+
   for (int i=0; i<5; ++i) {
−
path3 pentagon(real radius, real angle, triple center) {
+
     real a = i * angle;
−
  path3 p;
+
     pts.push(c + size * dir * dir(90+a));
−
   for (int i = 0; i <= 5; ++i) {
+
  }
−
     real ang = angle + i * 72;
+
 
−
     p = p -- (radius * cos(ang * pi / 180), radius * sin(ang * pi / 180), 0) + center;
+
  pts.push(pts[0]); // Close the loop
 +
 
 +
  for (int i=1; i<6; ++i) {
 +
    draw(pts[i-1]--pts[i], color);
 
   }
 
   }
−
  return p;
 
 
}
 
}
  
−
// Generate the central pentagon
+
currentprojection = orthographic(0.5,-1,0.2);
−
triple center = (0,0,0);
+
triple c = (0,0,0); // Center of dodecahedron
−
path3 centralPentagon = pentagon(1, 90, center);
+
real size = 1;
 +
 
 +
// Draw the central face
 +
drawPentagon(c, (0,0,1), size, blue);
  
−
// Function to rotate a path3 around an axis by a given angle
+
// Draw surrounding faces
−
path3 rotatePath3(path3 p, real angle, triple axis0, triple axis1) {
+
for (int i = 0; i < 5; ++i) {
−
   return rotate(angle, axis0, axis1) * p;
+
  real angle = i * 72;
 +
  triple dir = dir(90+angle);
 +
  triple offset = size * 1.618 * dir; // 1.618 is approx the golden ratio
 +
   drawPentagon(c+offset, (0,0,1), size, red);
 
}
 
}
  
−
// Create and draw the rotated pentagons
+
// Draw the outer pentagons,
 +
// offset a bit further than the middle pentagons
 
for (int i = 0; i < 5; ++i) {
 
for (int i = 0; i < 5; ++i) {
−
   real angle = 72 * i;
+
   real angle = i * 72 + 36; // offset by half angle to alternate
−
   path3 rotatedPentagon = rotatePath3(centralPentagon, angle, (0,0,0), (0,0,1));
+
   triple dir = dir(90+angle);
−
   draw(project(rotatedPentagon), linewidth(1bp));
+
   triple offset = size * 3 * dir;
−
   for (int j = 1; j < 6; ++j) {
+
   drawPentagon(c+offset, (0,0,1), size, green);
−
    rotatedPentagon = rotatePath3(rotatedPentagon, 72, (0,0,0), (0,0,1));
 
−
    draw(project(rotatedPentagon), linewidth(1bp));
 
−
  }
 
 
}
 
}
−
 
−
// Draw the central pentagon last to ensure it's on top
 
−
draw(project(centralPentagon), linewidth(1bp));
 
 
</asy>
 
</asy>
  

Revision as of 01:24, 25 November 2023

The following problem is from both the 2023 AMC 10A #25 and 2023 AMC 12A #21, so both problems redirect to this page.

Problem

If $A$ and $B$ are vertices of a polyhedron, define the distance $d(A,B)$ to be the minimum number of edges of the polyhedron one must traverse in order to connect $A$ and $B$. For example, if $\overline{AB}$ is an edge of the polyhedron, then $d(A, B) = 1$, but if $\overline{AC}$ and $\overline{CB}$ are edges and $\overline{AB}$ is not an edge, then $d(A, B) = 2$. Let $Q$, $R$, and $S$ be randomly chosen distinct vertices of a regular icosahedron (regular polyhedron made up of 20 equilateral triangles). What is the probability that $d(Q, R) > d(R, S)$?

$\textbf{(A) } \frac{7}{22} \qquad \textbf{(B) } \frac{1}{3} \qquad \textbf{(C) } \frac{3}{8} \qquad \textbf{(D) } \frac{5}{12} \qquad \textbf{(E) } \frac{1}{2}$

Solution 1

To find the total amount of vertices we first find the amount of edges, and that is $\frac{20 \times 3}{2}$. Next, to find the amount of vertices we can use Euler's characteristic, $V - E + F = 2$, and therefore the amount of vertices is $12$

So there are $P(12,3) = 1320$ ways to choose 3 distinct points.

Now, the furthest distance we can get from one point to another point in an icosahedron is 3. Which gives us a range of $1 \leq d(Q, R), d(R, S) \leq 3$

With some case work, we get two cases:

Case 1: $d(Q, R) = 3; d(R, S) = 1, 2$

Since we have only one way to choose Q, that is, the opposite point from R, we have one option for Q and any of the other points could work for S.

Then, we get $12 \times 1 \times 10 = 120$ (ways to choose R × ways to choose Q × ways to choose S)

Case 2: $d(Q, R) = 2; d(R, S) = 1$

We can visualize the icosahedron as 4 rows, first row with 1 vertex, second row with 5 vertices, third row with 5 vertices and fourth row with 1 vertex. We set R as the one vertex on the first row, and we have 12 options for R. Then, Q can be any of the 5 points on the third row and finally S can be one of the 5 points on the second row.

Therefore, we have $12 \times 5 \times 5 = 300$ (ways to choose R × ways to choose Q × ways to choose S)

Hence, $P(d(Q, R)>d(R, S)) = \frac{120+300}{1320} = \boxed{\textbf{(A) } \frac{7}{22}}$

~lptoggled, edited by ESAOPS and trevian1

Solution 2 (Cheese + Actual way)

In total, there are $\binom{12}{3}=220$ ways to select the points. However, if we look at the denominators of $B,C,D$, they are $3,8,12$ which are not divisors of $220$. Also $\frac{1}{2}$ is impossible as cases like $d(Q, R) = d(R, S)$ exist. The only answer choice left is $\boxed{\textbf{(A) } \frac{7}{22}}$

Note: this cheese is actually wrong because the total number of ways to select the points is actually $12 \times 11 \times 10 = 1320$ as order matters, so all denominators are possible. Rather, you can arrive at the same conclusion by fixing R WLOG, leading to $11 \times 10 = 110$ ways in total, which works for the original cheese. ~awesomeguy856

(Actual way)

Fix an arbitrary point, to select the rest $2$ points, there are $\binom{11}{2}=55$ ways. To make $d(Q, R)=d(R, S), d=1/2$. Which means there are in total $2\cdot \binom{5}{2}=20$ ways to make the distance the same. $\frac{1}{2}(1-\frac{20}{55})= \boxed{\textbf{(A) } \frac{7}{22}}$ ~bluesoul

Solution 3

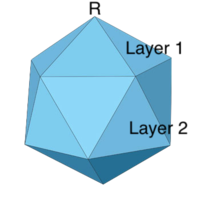
We can imagine the icosahedron as having 4 layers. 1 vertex at the top, 5 vertices below connected to the top vertex, 5 vertices below that which are 2 edges away from the top vertex, and one vertex at the bottom that is 3 edges away. WLOG because the icosahedron is symmetric around all vertices, we can say that R is the vertex at the top. So now, we just need to find the probability that S is on a layer closer to the top than Q. We can do casework on the layer S is on to get \[\frac{5}{11} \cdot \frac{6}{10} + \frac{5}{11} \cdot \frac{1}{10} = \frac{35}{110} = \frac{7}{22}\] So the answer is $\boxed{\textbf{(A) }\frac{7}{22}}$. -awesomeparrot

Solution 4

We can actually see that the probability that $d(Q, R) > d(R, S)$ is the exact same as $d(Q, R) < d(R, S)$ because $d(Q, R)$ and $d(R, S)$ have no difference. (In other words, we can just swap Q and S, meaning that can be called the same probability-wise.) Therefore, we want to find the probability that $d(Q, R) = d(R, S)$.

WLOG, we can rotate the icosahedron so that R is the top of the icosahedron. Then we can divide this into 2 cases:

1. They are on the second layer

There are 5 ways to put one point, and 4 ways to put the other point such that $d(Q, R) = d(R, S) = 1$. So, there are $5 \cdot 4 = 20$ ways to put them on the second layer.

2. They are on the third layer

There are 5 ways to put one point, and 4 ways to put the other point such that $d(Q, R) = d(R, S) = 2$. So, there are $5 \cdot 4 = 20$ ways to put them on the third layer.

The total number of ways to choose P and S are $11 \cdot 10 = 110$ (because there are 12 vertices), so the probability that $d(Q, R) = d(R, S)$ is $\frac{20+20}{110} = \frac{4}{11}$.

Therefore, the probability that $d(Q, R) > d(R, S)$ is $\frac{1 - \frac{4}{11}}{2} = \boxed{\textbf{(A) }\frac{7}{22}}$

~Ethanzhang1001

Solution 5

We know that there are $20$ faces. Each of those faces has $3$ borders (since each is a triangle), and each edge is used as a border twice (for each face on either side). Thus, there are $\dfrac{20\cdot3}2=30$ edges.

By Euler's formula, which states that $v-e+f=2$ for all convex polyhedra, we know that there are $2-f+e=12$ vertices.

The answer can be counted by first counting the number of possible paths that will yield $d(Q, R) > d(R, S)$ and dividing it by $12\cdot11\cdot10$ (or $\dbinom{12}3$, depending on the approach). In either case, one will end up dividing by $11$ somewhere in the denominator. We can then hope that there will be no factor of $11$ in the numerator (which would cancel the $11$ in the denominator out), and answer the only option that has an $11$ in the denominator: $\boxed{\textbf{(A) }\frac{7}{22}}$.

~Technodoggo

Additional note by "Fruitz": Note that one can eliminate $1/2$ by symmetry if you swap the ineq sign.

Another note by "andliu766": A shorter way to find the number of vertices and edges is to use the fact that the MAA logo is an icosahedron. :)

Solution 6 (Case Work)

2023AMC12AP21.png

WLOG, let R be at the top-most vertex of the icosahedron. There are $2$ cases where $d(Q, R) > d(R, S)$.

Case 1: $Q$ is at the bottom-most vertex

If $Q$ is at the bottom-most vertex, no matter where $S$ is, $d(Q, R) > d(R, S)$. The probability that $Q$ is at the bottom-most vertex is $\frac{1}{11}$

Case 2: $Q$ is at the second layer

If $Q$ is at the second layer, $S$ must be at the first layer, for $d(Q, R) > d(R, S)$ to be true. The probability that $Q$ is at the second layer, and $S$ is at the first layer is $\frac{5}{11} \cdot \frac{5}{10} = \frac{5}{22}$

\[\frac{1}{11} + \frac{5}{22} = \boxed{\textbf{(A) }\frac{7}{22}}\]

~isabelchen

Solution 7 (efficient)

Since the icosahedron is symmetric polyhedron, we can rotate it so that R is on the topmost vertex. Since Q and S basically the same, we can first count the probability that $d(Q,R) = d(R,S)$.

$\mathfrak{Case} \ \mathfrak{1}: d(Q,R) = d(R,S) = 1$

There are 5 points $P$ such that $d(Q,P) = 1$. There is $5 \times 4 = \boxed{20}$ ways to choose Q and S in this case.

$\mathfrak{Case} \ \mathfrak{2}: d(Q,R) = d(R,S) = 2$

There are 5 points $P$ such that $d(Q,P) = 2$. There is $5 \times 4 = \boxed{20}$ ways to choose Q and S in this case.

$\mathfrak{Case} \ \mathfrak{3}: d(Q,R) = d(R,S) = 3$

There is 1 point $P$ such that $d(Q,P) = 3$. There is $1 \times 0 = \boxed{0}$ ways to choose Q and S in this case.

$\mathfrak{Final} \ \mathfrak{solution}$

There are 11 points $P$ that are distinct from R. There is $11 \times 10 = \boxed{110}$ ways to choose Q and S. There is $20 + 20 + 0 = \boxed{40}$ ways to choose Q and S such that $d(Q,R) = d(R,S)$. There is $\frac{110-40}{2} = 35$ ways to choose Q and S such that $d(Q, R) > d(R, S)$. The probability that $d(Q, R) > d(R, S)$ is therefore $\frac{35}{110} = \frac{7}{22}$ which corresponds to answer choice $\boxed{A}$

~~afly

Solution 8 (Dodecahedron Schlegel Diagram)

import three;

// Definition for drawing pentagon
void drawPentagon(triple c, triple dir, real size, pen color) {
  real angle = 72;
  triple[] pts;

  for (int i=0; i<5; ++i) {
    real a = i * angle;
    pts.push(c + size * dir * dir(90+a));
  }
  
  pts.push(pts[0]); // Close the loop

  for (int i=1; i<6; ++i) {
    draw(pts[i-1]--pts[i], color);
  }
}

currentprojection = orthographic(0.5,-1,0.2);
triple c = (0,0,0); // Center of dodecahedron
real size = 1;

// Draw the central face
drawPentagon(c, (0,0,1), size, blue);

// Draw surrounding faces
for (int i = 0; i < 5; ++i) {
  real angle = i * 72;
  triple dir = dir(90+angle);
  triple offset = size * 1.618 * dir; // 1.618 is approx the golden ratio
  drawPentagon(c+offset, (0,0,1), size, red);
}

// Draw the outer pentagons,
// offset a bit further than the middle pentagons
for (int i = 0; i < 5; ++i) {
  real angle = i * 72 + 36; // offset by half angle to alternate
  triple dir = dir(90+angle);
  triple offset = size * 3 * dir;
  drawPentagon(c+offset, (0,0,1), size, green);
}
 (Error making remote request. Unknown error_msg)

Video Solution by OmegaLearn

https://youtu.be/Wc6PFNq5PAM

1 minute solution by MegaMath

https://www.youtube.com/watch?v=dxYw1wYHid4&t=12s

~megahertz13

Video Solution by epicbird08

https://youtu.be/s_6q0C0z6Ug

~EpicBird08

Vide Solution by SpreadTheMathLove(Casework and Complementary)

https://www.youtube.com/watch?v=4FEwxwgbliQ

Video Solution

https://youtu.be/bS3tle-jP4g

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Video Solution by TheBeautyofMath

https://youtu.be/ZvrlZ2NoH8s

~IceMatrix

See also

2023 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 24 		Followed by
Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
2023 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 20 		Followed by
Problem 22
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2023_AMC_12A_Problems/Problem_21&oldid=205692"