Difference between revisions of "2006 AMC 12A Problems/Problem 19"
m (→Solution: -{{sol}}) |
m |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
| − | |||
| − | |||
| − | |||
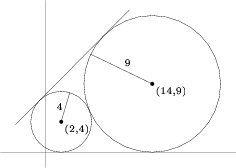
[[Circle]]s with [[center]]s <math>(2,4)</math> and <math>(14,9)</math> have [[radius | radii]] <math>4</math> and <math>9</math>, respectively. The equation of a common external [[tangent line|tangent]] to the circles can be written in the form <math>y=mx+b</math> with <math>m>0</math>. What is <math>b</math>? | [[Circle]]s with [[center]]s <math>(2,4)</math> and <math>(14,9)</math> have [[radius | radii]] <math>4</math> and <math>9</math>, respectively. The equation of a common external [[tangent line|tangent]] to the circles can be written in the form <math>y=mx+b</math> with <math>m>0</math>. What is <math>b</math>? | ||
| + | <center>[[Image:AMC12_2006A_19.png]]</center> | ||
<math> \mathrm{(A) \ } \frac{908}{199}\qquad \mathrm{(B) \ } \frac{909}{119}\qquad \mathrm{(C) \ } \frac{130}{17}\qquad \mathrm{(D) \ } \frac{911}{119}</math><math>\mathrm{(E) \ } \frac{912}{119}</math> | <math> \mathrm{(A) \ } \frac{908}{199}\qquad \mathrm{(B) \ } \frac{909}{119}\qquad \mathrm{(C) \ } \frac{130}{17}\qquad \mathrm{(D) \ } \frac{911}{119}</math><math>\mathrm{(E) \ } \frac{912}{119}</math> | ||
Revision as of 18:29, 8 November 2007
Problem
Circles with centers ![]() and
and ![]() have radii
have radii ![]() and
and ![]() , respectively. The equation of a common external tangent to the circles can be written in the form
, respectively. The equation of a common external tangent to the circles can be written in the form ![]() with
with ![]() . What is
. What is ![]() ?
?
![]()
![]()
Solution
- This solution needs a clearer explanation and a diagram.
Notice that both circles are tangent to the x-axis and each other. Call the circles (respectively) A and B; the distance between the two centers is ![]() . If we draw the parallel radii that lead to the common external tangent, a line can be extended parallel to the tangent from A to the radius of circle B. This creates a 5-12-13 triangle. To find the slope of that line (which is parallel to the tangent), note that another 5-12-13 triangle can be drawn below the first one such that the side with length 12 is parallel to the x-axis. The slope can be found by using the double tangent identity,
. If we draw the parallel radii that lead to the common external tangent, a line can be extended parallel to the tangent from A to the radius of circle B. This creates a 5-12-13 triangle. To find the slope of that line (which is parallel to the tangent), note that another 5-12-13 triangle can be drawn below the first one such that the side with length 12 is parallel to the x-axis. The slope can be found by using the double tangent identity,
To find the x and y coordinates of the point of tangency of circle A, we can set up a ratio (the slope will be –119/120 because it is the negative reciprocal):
We can plug this into the equation of the line for the tangent to get:
See also
| 2006 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 18 |
Followed by Problem 20 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |









