Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2022 AIME II Problems/Problem 2"

m
m (→‎Solution 1)
Line 11: Line 11:
 
This problem can be solved by using <math>2</math> cases.
 
This problem can be solved by using <math>2</math> cases.
  
−
<math>\textbf{Case 1:}</math> <math>C</math>'s opponent for the semifinals is <math>A</math>
+
<math>\textbf{Case 1:}</math> <math>C</math>'s opponent for the semifinal is <math>A</math>
  
−
The probability <math>C</math>'s opponent is <math>A</math> is <math>\frac13</math>. Therefore the probability <math>C</math> wins the semifinals in this case is <math>\frac13 \cdot \frac13</math>. The other semifinal game is played between <math>J</math> and <math>S</math>, it doesn't matter who wins because <math>C</math> has the same probability of winning either one. The probability of <math>C</math> winning in the finals is <math>\frac34</math>, so the probability of <math>C</math> winning the tournament in case 1 is <math>\frac13 \cdot \frac13 \cdot \frac34</math>
+
The probability <math>C</math>'s opponent is <math>A</math> is <math>\frac13</math>. Therefore the probability <math>C</math> wins the semifinal in this case is <math>\frac13 \cdot \frac13</math>. The other semifinal game is played between <math>J</math> and <math>S</math>, it doesn't matter who wins because <math>C</math> has the same probability of winning either one. The probability of <math>C</math> winning in the final is <math>\frac34</math>, so the probability of <math>C</math> winning the tournament in case 1 is <math>\frac13 \cdot \frac13 \cdot \frac34</math>
  
  
−
<math>\textbf{Case 2:}</math> <math>C</math>'s opponent for the semifinals is <math>J</math> or <math>S</math>
+
<math>\textbf{Case 2:}</math> <math>C</math>'s opponent for the semifinal is <math>J</math> or <math>S</math>
  
−
It doesn't matter if <math>C</math>'s opponent is <math>J</math> or <math>S</math> because <math>C</math> has the same probability of winning either one. The probability <math>C</math>'s opponent is <math>J</math> or <math>S</math> is <math>\frac23</math>. Therefore the probability <math>C</math> wins the semifinals in this case is <math>\frac23 \cdot \frac34</math>. The other semifinal game is played between <math>A</math> and <math>J</math> or <math>S</math>. In this case it matters who wins in the other semifinal game because the probability of <math>C</math> winning <math>A</math> and <math>J</math> or <math>S</math> is different.  
+
It doesn't matter if <math>C</math>'s opponent is <math>J</math> or <math>S</math> because <math>C</math> has the same probability of winning either one. The probability <math>C</math>'s opponent is <math>J</math> or <math>S</math> is <math>\frac23</math>. Therefore the probability <math>C</math> wins the semifinal in this case is <math>\frac23 \cdot \frac34</math>. The other semifinal game is played between <math>A</math> and <math>J</math> or <math>S</math>. In this case it matters who wins in the other semifinal game because the probability of <math>C</math> winning <math>A</math> and <math>J</math> or <math>S</math> is different.  
  
−
<math>\textbf{Case 2.1:}</math> <math>C</math>'s opponent for the finals is <math>A</math>
+
<math>\textbf{Case 2.1:}</math> <math>C</math>'s opponent for the final is <math>A</math>
  
−
For this to happen, <math>A</math> must have won <math>J</math> or <math>S</math> in the semifinals, the probability is <math>\frac34</math>. Therefore, the probability that <math>C</math> won <math>A</math> in the finals is <math>\frac34 \cdot \frac13</math>.
+
For this to happen, <math>A</math> must have won <math>J</math> or <math>S</math> in the semifinal, the probability is <math>\frac34</math>. Therefore, the probability that <math>C</math> won <math>A</math> in the final is <math>\frac34 \cdot \frac13</math>.
  
−
<math>\textbf{Case 2.1:}</math> <math>C</math>'s opponent for the finals is <math>J</math> or <math>S</math>
+
<math>\textbf{Case 2.1:}</math> <math>C</math>'s opponent for the final is <math>J</math> or <math>S</math>
  
−
For this to happen, <math>J</math> or <math>S</math> must have won <math>A</math> in the semifinals, the probability is <math>\frac14</math>. Therefore, the probability that <math>C</math> won <math>J</math> or <math>S</math> in the finals is <math>\frac14 \cdot \frac34</math>.
+
For this to happen, <math>J</math> or <math>S</math> must have won <math>A</math> in the semifinal, the probability is <math>\frac14</math>. Therefore, the probability that <math>C</math> won <math>J</math> or <math>S</math> in the final is <math>\frac14 \cdot \frac34</math>.
  
 
In Case 2 the probability of <math>C</math> winning the tournament is <math>\frac23 \cdot \frac34 \cdot (\frac34 \cdot \frac13 + \frac14 \cdot \frac34)</math>
 
In Case 2 the probability of <math>C</math> winning the tournament is <math>\frac23 \cdot \frac34 \cdot (\frac34 \cdot \frac13 + \frac14 \cdot \frac34)</math>

Revision as of 03:25, 19 February 2022

Problem

Azar, Carl, Jon, and Sergey are the four players left in a singles tennis tournament. They are randomly assigned opponents in the semifinal matches, and the winners of those matches play each other in the final match to determine the winner of the tournament. When Azar plays Carl, Azar will win the match with probability $\frac23$. When either Azar or Carl plays either Jon or Sergey, Azar or Carl will win the match with probability $\frac34$. Assume that outcomes of different matches are independent. The probability that Carl will win the tournament is $\frac{p}{q}$, where $p$ and $q$ are relatively prime positive integers. Find $p+q$.

Solution 1

Let $A$ be Azar, $C$ be Carl, $J$ be Jon, and $S$ be Sergey. The $4$ circles represent the $4$ players, and the arrow is from the winner to the loser with the winning probability as the label.

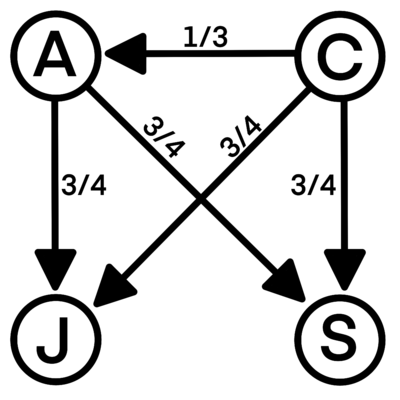
2022AIMEIIP2.png

This problem can be solved by using $2$ cases.

$\textbf{Case 1:}$ $C$'s opponent for the semifinal is $A$

The probability $C$'s opponent is $A$ is $\frac13$. Therefore the probability $C$ wins the semifinal in this case is $\frac13 \cdot \frac13$. The other semifinal game is played between $J$ and $S$, it doesn't matter who wins because $C$ has the same probability of winning either one. The probability of $C$ winning in the final is $\frac34$, so the probability of $C$ winning the tournament in case 1 is $\frac13 \cdot \frac13 \cdot \frac34$


$\textbf{Case 2:}$ $C$'s opponent for the semifinal is $J$ or $S$

It doesn't matter if $C$'s opponent is $J$ or $S$ because $C$ has the same probability of winning either one. The probability $C$'s opponent is $J$ or $S$ is $\frac23$. Therefore the probability $C$ wins the semifinal in this case is $\frac23 \cdot \frac34$. The other semifinal game is played between $A$ and $J$ or $S$. In this case it matters who wins in the other semifinal game because the probability of $C$ winning $A$ and $J$ or $S$ is different.

$\textbf{Case 2.1:}$ $C$'s opponent for the final is $A$

For this to happen, $A$ must have won $J$ or $S$ in the semifinal, the probability is $\frac34$. Therefore, the probability that $C$ won $A$ in the final is $\frac34 \cdot \frac13$.

$\textbf{Case 2.1:}$ $C$'s opponent for the final is $J$ or $S$

For this to happen, $J$ or $S$ must have won $A$ in the semifinal, the probability is $\frac14$. Therefore, the probability that $C$ won $J$ or $S$ in the final is $\frac14 \cdot \frac34$.

In Case 2 the probability of $C$ winning the tournament is $\frac23 \cdot \frac34 \cdot (\frac34 \cdot \frac13 + \frac14 \cdot \frac34)$

Adding case 1 and case 2 together we get $\frac13 \cdot \frac13 \cdot \frac34 + \frac23 \cdot \frac34 \cdot (\frac34 \cdot \frac13 + \frac14 \cdot \frac34) = \frac{29}{96}$. So the answer is $29 + 96 = \boxed{\textbf{125}}$

~isabelchen

Video Solution (Mathematical Dexterity)

https://www.youtube.com/watch?v=C14f91P2pYc

See Also

2022 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 1 		Followed by
Problem 3
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2022_AIME_II_Problems/Problem_2&oldid=171524"