Pascal's Identity

Identity

Pascal's Identity states that

${n \choose k}={n-1\choose k-1}+{n-1\choose k}$

for any positive integers $k$ and $n$ . Here, $\binom{n}{k}$ is the binomial coefficient $\binom{n}{k} = nCk = C_k^n$ .

Remember that $\binom{n}{r}=\frac{n!}{k!(n-k)!}.$

Proving it

If $k > n$ then $\binom{n}{k} = 0 = \binom{n - 1}{k - 1} + \binom{n - 1}{k}$ and so the result is pretty clear. So assume $k \leq n$ . Then

$\begin{eqnarray*}\binom{n-1}{k-1}+\binom{n-1}{k}&=&\frac{(n-1)!}{(k-1)!(n-k)!}+\frac{(n-1)!}{k!(n-k-1)!}\\ &=&(n-1)!\left(\frac{k}{k!(n-k)!}+\frac{n-k}{k!(n-k)!}\right)\\ &=&(n-1)!\cdot \frac{n}{k!(n-k)!}\\ &=&\frac{n!}{k!(n-k)!}\\ &=&\binom{n}{k}. \qquad\qquad\square\end{eqnarray*}$ There we go. We proved it!

Why is it needed?

It's mostly just a cool thing to know. However, if you want to know how to use it in real life go to https://artofproblemsolving.com/videos/counting/chapter12/141. Or really any of the counting and probability videos.

Introduction to Pascal's Triangle

How to build it

Pascal's Triangle is a triangular array of numbers in which you start with two infinite diagonals of ones and each of the rest of the numbers is the sum of the two numbers above it. It looks something like this:

And on and on...

Combinations

Pascal's Triangle is really combinations. It looks something like this if it is depicted as combinations:

And on and on...

Proof

If you look at the way we build the triangle, each number is the sum of the two numbers above it. Assuming that these combinations are true then each combination in the sum of the two combinations above it. In an equation, it would look something like this: ${n \choose k}={n-1\choose k-1}+{n-1\choose k}$ . It's Pascals Identity! Therefore each row looks something like this:

$\binom{n}{0} \binom{n}{1} \binom{n}{2} ... \binom{n}{n}$

Patterns and Properties

In addition to combinations, Pascal's Triangle has many more patterns and properties. See below. Be ready to be amazed.

Binomial Theorem

Let's multiply out some binomials. Try it yourself and it will not be fun: $(x+y)^0=1$

$(x+y)^1=1x+1y$

$(x+y)^2=1x^2+2xy+1y^2$

$(x+y)^2=1x^3+3x^2y+3y^2x+1^3$

If you take away the x's and y's you get:

It's Pascal's Triangle!

Proof

There are a number of different ways to prove the Binomial Theorem, for example by a straightforward application of mathematical induction. The Binomial Theorem also has a nice combinatorial proof:

We can write $(a+b)^n=\underbrace{ (a+b)\cdot(a+b)\cdot(a+b)\cdot\cdots\cdot(a+b) }_{n}$ . Repeatedly using the distributive property, we see that for a term $a^m b^{n-m}$ , we must choose $m$ of the $n$ terms to contribute an $a$ to the term, and then each of the other $n-m$ terms of the product must contribute a $b$ . Thus, the coefficient of $a^m b^{n-m}$ is the number of ways to choose $m$ objects from a set of size $n$ , or $\binom{n}{m}$ . Extending this to all possible values of $m$ from $0$ to $n$ , we see that $(a+b)^n = \sum_{m=0}^{n}{\binom{n}{m}}\cdot a^m\cdot b^{n-m}$ , as claimed.

Similarly, the coefficients of $(x+y)^n$ will be the entries of the $n^\text{th}$ row of Pascal's Triangle. This is explained further in the Counting and Probability textbook [AoPS]

In real life

It is really only used for multipling out binomials. More usage at https://artofproblemsolving.com/videos/counting/chapter14/126.

Powers of 2

Theorem

It states that $\binom{n}{0}+\binom{n}{1}+...+\binom{n}{n}=2^n$

Why do we need it?

It is useful in many word problems (That means, yes, you can use it in real life) and it is just a cool thing to know. More at https://artofproblemsolving.com/videos/mathcounts/mc2010/419.

Proof

Subset proof

Say you have a word with n letters. How many subsets does it have in terms of n? Here is how you answer it: You ask the first letter Are you in or are you out? Same to the second letter. Same to the third. Same to the n. Each of the letters has two choices: In and Out. The would be $(2)(2)(2)(2)$ ...n times. $2^n$ .

Alternate proof

If you look at the way we built the triangle you see that each number is row n-1 is added on twice in row n. This means that each row doubles. That means you get powers of two.

Triangle Numbers

Theorem

If you look at the numbers in the third diagonal you see that they are triangle numbers.

Proof

Now we can make an equation: $\binom{n}{2}=1+2+3+...+(n-1) \Rightarrow \binom{n}{2}=\frac{n(n+1)}{2} \Rightarrow \frac{n!}{2!(n-2)!}=\frac{n(n+1)}{2} \Rightarrow \frac{n(n+1)}{2}=\frac{n(n+1)}{2}$

Hockey stick

For $n,r\in\mathbb{N}, n>r,\sum^n_{i=r}{i\choose r}={n+1\choose r+1}$ .

$[asy] int chew(int n,int r){ int res=1; for(int i=0;i<r;++i){ res=quotient(res*(n-i),i+1); } return res; } for(int n=0;n<9;++n){ for(int i=0;i<=n;++i){ if((i==2 && n<8)||(i==3 && n==8)){ if(n==8){label(string(chew(n,i)),(11+n/2-i,-n),p=red+2.5);} else{label(string(chew(n,i)),(11+n/2-i,-n),p=blue+2);} } else{ label(string(chew(n,i)),(11+n/2-i,-n)); } } } [/asy]$

This identity is known as the hockey-stick identity because, on Pascal's triangle, when the addends represented in the summation and the sum itself is highlighted, a hockey-stick shape is revealed.

Proof

Inductive Proof

This identity can be proven by induction on $n$ .

Base Case Let $n=r$ .

$\sum^n_{i=r}{i\choose r}=\sum^r_{i=r}{i\choose r}={r\choose r}=1={r+1\choose r+1}$ .

Inductive Step Suppose, for some $k\in\mathbb{N}, k>r$ , $\sum^k_{i=r}{i\choose r}={k+1\choose r+1}$ . Then $\sum^{k+1}_{i=r}{i\choose r}=\left(\sum^k_{i=r}{i\choose r}\right)+{k+1\choose r}={k+1\choose r+1}+{k+1\choose r}={k+2\choose r+1}$ .

Algebraic Proof

It can also be proven algebraically with Pascal's Identity, ${n \choose k}={n-1\choose k-1}+{n-1\choose k}$ . Note that

${r \choose r}+{r+1 \choose r}+{r+2 \choose r}+\cdots+{r+a \choose r}$ $={r+1 \choose r+1}+{r+1 \choose r}+{r+2 \choose r}+\cdots+{r+a \choose r}$ $={r+2 \choose r+1}+{r+2 \choose r}+\cdots+{r+a \choose r}=\cdots={r+a \choose r+1}+{r+a \choose r}={r+a+1 \choose r+1}$ , which is equivalent to the desired result.

Combinatorial Proof 1

Imagine that we are distributing $n$ indistinguishable candies to $k$ distinguishable children. By a direct application of Balls and Urns, there are ${n+k-1\choose k-1}$ ways to do this. Alternatively, we can first give $0\le i\le n$ candies to the oldest child so that we are essentially giving $n-i$ candies to $k-1$ kids and again, with Balls and Urns, ${n+k-1\choose k-1}=\sum_{i=0}^n{n+k-2-i\choose k-2}$ , which simplifies to the desired result.

Combinatorial Proof 2

We can form a committee of size $k+1$ from a group of $n+1$ people in ${{n+1}\choose{k+1}}$ ways. Now we hand out the numbers $1,2,3,\dots,n-k+1$ to $n-k+1$ of the $n+1$ people. We can divide this into $n-k+1$ disjoint cases. In general, in case $x$ , $1\le x\le n-k+1$ , person $x$ is on the committee and persons $1,2,3,\dots, x-1$ are not on the committee. This can be done in $\binom{n-x+1}{k}$ ways. Now we can sum the values of these $n-k+1$ disjoint cases, getting ${{n+1}\choose {k+1}} ={{n}\choose{k}}+{{n-1}\choose{k}}+{{n-2}\choose{k}}+\hdots+{{k+1}\choose{k}}+{{k}\choose{k}}.$

Copied From

- 50 percent original made by Colball otherwise known as Colin Friesen

- Pascal's Identity

- Hockey-Stick Identity

- Pascal's Triangle

These are all on AoPS wiki. Look them up.

Now to Pythagorean Theorem.

What is the Pythagorean Theorem?

The Pythagoras Theorem is also referred to as the Pythagorean Theorem $.$ Pythagorean Theorem is used to find a side of any right triangle. It is $a^2+b^2=c^2$ , where $a$ and $b$ are the legs of the triangle, and $c$ is the hypotenuse.

Why is it useful?

To find sides and angles of right triangles. Also, Trigonometry is pointless without it. If you know three angles of a triangle you can use the Pythagorean Theorem to find the sides or the area even if the angles are not right. It is probably the most famous Theorem in all of math!

Can we prove it?

Yes! The are hundreds of proves. I will just show you a few of them. Mathematicians even make a hobby of finding these proves. Even a US president made a published proof! Of, course this was a president in the 1800s because, well, presidents now are not really up to proving something like that. (You know, Trump and the others).

Proofs

Proof 1

We use $[ABC]$ to denote the area of triangle $ABC$ .

Let $H$ be the perpendicular to side $AB$ from ${} C$ .

$[asy] pair A, B, C, H; A = (0, 0); B = (4, 3); C = (4, 0); H = foot(C, A, B); draw(A--B--C--cycle); draw(C--H); draw(rightanglemark(A, C, B)); draw(rightanglemark(C, H, B)); label("$A$", A, SSW); label("$B$", B, ENE); label("$C$", C, SE); label("$H$", H, NNW); [/asy]$

Since $ABC, CBH, ACH$ are similar right triangles, and the areas of similar triangles are proportional to the squares of corresponding side lengths,

$\frac{[ABC]}{AB^2} = \frac{[CBH]}{CB^2} = \frac{[ACH]}{AC^2}$ .

But since triangle $ABC$ is composed of triangles $CBH$ and $ACH$ , $[ABC] = [CBH] + [ACH]$ , so $AB^2 = CB^2 + AC^2$ . ∎

Proof 2

Consider a circle $\omega$ with center $B$ and radius $BC$ . Since $BC$ and $AC$ are perpendicular, $AC$ is tangent to $\omega$ . Let the line $AB$ meet $\omega$ at $Y$ and $X$ , as shown in the diagram:

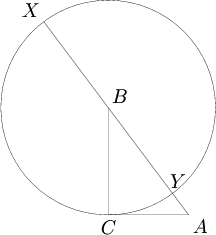
Evidently, $AY = AB - BC$ and $AX = AB + BC$ . By considering the power of point $A$ with respect to $\omega$ , we see

$AC^2 = AY \cdot AX = (AB-BC)(AB+BC) = AB^2 - BC^2$ . ∎

Proof 3

$ABCD$ and $EFGH$ are squares.

$[asy] pair A, B,C,D; A = (-10,10); B = (10,10); C = (10,-10); D = (-10,-10); pair E,F,G,H; E = (7,10); F = (10, -7); G = (-7, -10); H = (-10, 7); draw(A--B--C--D--cycle); label("$A$", A, NNW); label("$B$", B, ENE); label("$C$", C, ESE); label("$D$", D, SSW); draw(E--F--G--H--cycle); label("$E$", E, N); label("$F$", F,SE); label("$G$", G, S); label("$H$", H, W); label("a", A--B,N); label("a", B--F,SE); label("a", C--G,S); label("a", H--D,W); label("b", E--B,N); label("b", F--C,SE); label("b", G--D,S); label("b", A--H,W); label("c", E--H,NW); label("c", E--F); label("c", F--G,SE); label("c", G--H,SW); [/asy]$

$(a+b)^2=c^2+4\left(\frac{1}{2}ab\right)\implies a^2+2ab+b^2=c^2+2ab\implies a^2 + b^2=c^2$ . ∎

Pythagorean Triples

Pythagorean Triples are a group of integers a,b and c in which $a^2+b^2=c^2$ . These are the first few: (3,4,5) (5,12,13) (7,24,25) (8,15,17)

(9,40,41) (11,60,61) (12,35,37) (13,84,85)

(15,112,113) (16,63,65) (17,144,145) (19,180,181)

(20,21,29) (20,99,101) (21,220,221) (23,264,265)

(24,143,145) (25,312,313) (27,364,365) (28,45,53)

(28,195,197) (29,420,421) (31,480,481) (32,255,257)

(33,56,65) (33,544,545) (35,612,613) (36,77,85)

(36,323,325) (37,684,685)

And on and on... Remember that if $a^2+b^2=c^2$ then $xa^2+xb^2=xc^2$ so I did not include 6,8,10 or 10,24,26.

Special Right triangles

45-90-45

Theorem

Say you have a right triangle with angles 45, 45 and 90. Then if $a$ (leg) is $x$ , then $c$ (long side) is $x\sqrt2$

Proof

If this triangle has two equal angles then it has two equal sides. Therefore we can make an equation: $x^2+x^2=s^2$ . $s$ means side and is the hypotenuse. $x^2+x^2=s^2 \Rightarrow 2x^2=s^2 \Rightarrow \sqrt{2}x=s$ . We proved it!

30-60-90

Theorem

If the angles of a right triangle are 30, 60 and 90, and if the short side is $x$ then the long side is $2x$ and the other leg is $x\sqrt{3}$ .

Proof

The long side is clearly $2x$ because of the angles that are twice the size, so we can make an equation: $x^2+t^2=2x^2$ . t is the other leg.

$x^2+t^2=(2x)^2 \Rightarrow t^2=(2x)^2-x^2 \Rightarrow t^2=3x^2 \Rightarrow t=\sqrt{3}x$ We proved it!

Pythagorean Theorem related word problems

Problem 1

Hawick is 15 miles south of Abbotsford, and Kelso is 17 miles east of Abbotsford. What is the distance from Hawick to Kelso?

Solution

$15^2+17^2=x^2 \Rightarrow 514=x^2 \Rightarrow x=\sqrt{514}$

Problem 2

A zip line starts on a platform that is 40 feet above the ground. The anchor for the zip line is 198 horizontal feet from the base of the platform. How long is the zip line?

Solution

$40^2+198^2=x^2 \Rightarrow 40804=x^2 \Rightarrow x=202$

Page

Toolbox

Search

Pascal's Triangle and Pythagorean Theorem

Contents

Pascal's Identity

Identity

Proving it

Why is it needed?

Introduction to Pascal's Triangle

How to build it

Combinations

Combinations

Proof

Patterns and Properties

Binomial Theorem

Proof

In real life

Powers of 2

Theorem

Theorem

Why do we need it?

Proof

Subset proof

Alternate proof

Triangle Numbers

Theorem

Proof

Hockey stick

Proof

See Also

AoPS Wiki

Videos

Copied From

What is the Pythagorean Theorem?

What is the Pythagorean Theorem?

Why is it useful?

Can we prove it?

Proofs

Proof 1

Proof 2

Proof 3

Pythagorean Triples

Special Right triangles

45-90-45

Theorem

Proof

30-60-90

Theorem

Proof

Pythagorean Theorem related word problems

Problem 1

Solution

Problem 2

Solution