Cross-Segment Identity
Motivation
After repetitive usage of this in AMC/AIME Euclidean Geometry problems, I (mathboy282) only found it fit to make it an identity.
Identity
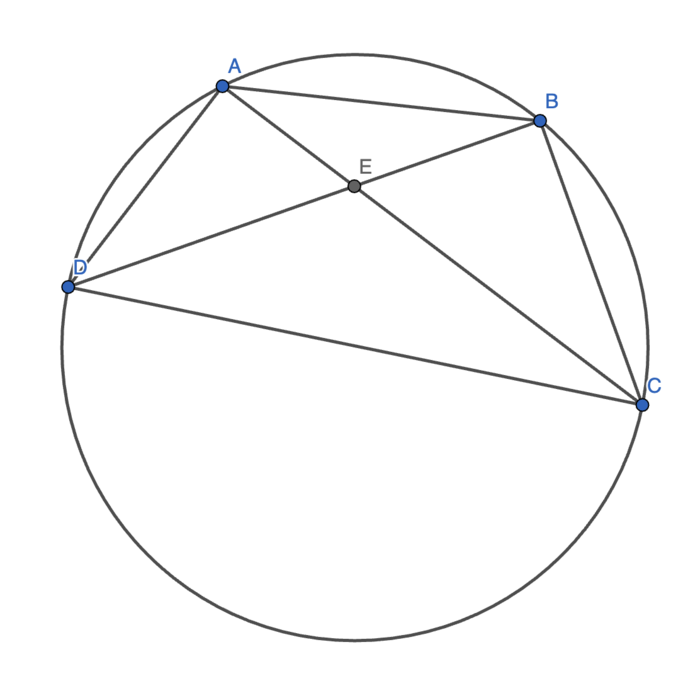
Let there be a cyclic quadrilateral ![]() with
with ![]() as the intersection of the diagonals
as the intersection of the diagonals ![]() and
and ![]()
Let ![]() and
and ![]() Then, we must have:
Then, we must have:
![]()
Proof
This comes as a direct result of Ptolemy's theorem.
![]()