2025 AIME II Problems/Problem 14

Problem

Let ${\triangle ABC}$ be a right triangle with $\angle A = 90^\circ$ and $BC = 38.$ There exist points $K$ and $L$ inside the triangle such $AK = AL = BK = CL = KL = 14.$ The area of the quadrilateral $BKLC$ can be expressed as $n\sqrt3$ for some positive integer $n.$ Find $n.$

Solution 1

From the given condition, we could get $\angle{LAK}=60^{\circ}$ and $\triangle{LCA}, \triangle{BAK}$ are isosceles. Denote $\angle{BAK}=\alpha, \angle{CAL}=30^{\circ}-\alpha$ . From the isosceles condition, we have $\angle{BKA}=180^{\circ}-2\alpha, \angle{CLA}=120^{\circ}-2\alpha$

Since $\angle{CAB}$ is right, then $AB^2+AC^2=BC^2$ , we could use law of cosines to express $AC^2, AB^2, AC^2+AB^2=2\cdot 14^2(2-\cos \angle{BKA}-\angle {CLA})=2\cdot 14^2(2+\cos(2\alpha)+\cos(60^{\circ}-2\alpha))=38^2$

Which simplifies to $\cos(2\alpha)+\cos(60^{\circ}-2\alpha)=\frac{165}{98}$ , expand the expression by angle subtraction formula, we could get $\sqrt{3}\sin(2\alpha+60^{\circ})=\frac{165}{98}, \sin(2\alpha+60^{\circ})=\frac{55\sqrt{3}}{98}$

Conenct $CK$ we could notice $\angle{CLA}=360^{\circ}-\angle{CLA}-\angle{ALK}=180^{\circ}-2\alpha=\angle{AKB}$ , since $CL=LK=AK=KB$ we have $\triangle{CLK}\cong \triangle{AKB}$ . Moreover, since $K$ lies on the perpendicular bisector of $AB$ , the distance from $K$ to $AC$ is half of the length of $AB$ , which means $[ACK]=\frac{[ABC]}{2}$ , and we could have $[ACK]=[ACL]+[ALK]+[ABK]=[ABC]-[BKLC]$ , so $[BKLC]=[AKC]$ . We have $[AKC]=[ALK]+\frac{14^2}{2}(\sin(60-2\alpha)+\sin \alpha)=98(\sin(60+2\alpha))+[ALK]=55\sqrt{3}+\frac{\sqrt{3}}{4}14^2=104\sqrt{3}$ , so our answer is $\boxed{104}$

~ Bluesoul

Solution 2

$[asy] import math; import geometry; import olympiad; point A,C,B,L,K,D,F,G,O; A=(0,0); C=(16sqrt(3),0); B=(0,26); L=(8sqrt(3),2); K=(3sqrt(3),13); D=(16sqrt(3),26); F=(13sqrt(3),13); G=(8sqrt(3),24); O=(8sqrt(3),13); draw(A--B--D--C--A--L--C--F--L--K--A--D); draw(K--B--G--D--F--G--K--F); draw(B--O--L); draw(C--O--G); label("A",A,SW); label("B",B,NW); label("C",C,SE); label("A'",D,NE); label("K",K,W); label("L",L,NW); label("L'",G,SE); label("K'",F,E); label("O",O,NNW); [/asy]$ Let $O$ be the midpoint of $BC$ . Take the diagram and rotate it $180^{\circ}$ around $O$ to get the diagram shown. Notice that we have $\angle ABC+\angle ACB=90^{\circ}$ . Because $\triangle AKL$ is equilateral, then $\angle KAL=60^{\circ}$ , so $\angle BAK+\angle CAL=30^{\circ}$ . Because of isosceles triangles $\triangle BAK$ and $\triangle CAL$ , we get that $\angle ABK+\angle ACL=30^{\circ}$ too, implying that $\angle KBC+\angle LCB=60^{\circ}$ . But by our rotation, we have $\angle LCO=\angle L'BO$ , so this implies that $\angle KBL'=60^{\circ}$ , or that $\triangle KBL'$ is equilateral. We can similarly derive that $\angle KBO=\angle K'CO$ implies $\angle LCK'=60^{\circ}$ so that $\triangle LK'C$ is also equilateral. At this point, notice that quadrilateral $KL'K'L$ is a rhombus. The area of our desired region is now $[BKLC]=\frac{1}{2}[BL'K'CLK]$ . We can easily find the areas of $\triangle KBL'$ and $\triangle LK'C$ to be $\frac{\sqrt{3}}{4}\cdot 14^2=49\sqrt{3}$ . Now it remains to find the area of rhombus $KL'K'L$ . $[asy] import math; import geometry; import olympiad; point A,K,O,L,M; A=(-7sqrt(3),0); K=(0,7); O=(55sqrt(3)/14,23/14); L=(0,-7); M=(0,0); draw(A--K--O--L--A--O--M--A); draw(K--L); label("A",A,W); label("K",K,N); label("O",O,E); label("L",L,S); label("M",M,SE); [/asy]$ Focus on the quadrilateral $AKOL$ . Restate the configuration in another way - we have equilateral triangle $\triangle AKL$ with side length 14, and a point $O$ such that $AO=19$ and $\angle KOL=90^{\circ}$ . We are trying to find the area of $\triangle KOL$ . Let $M$ be the midpoint of $KL$ . We see that $AM=7\sqrt{3}$ , and since $M$ is the circumcenter of $\triangle KOL$ , it follows that $MO=7$ . Let $\angle KMO=\theta$ . From the Law of Cosines in $\triangle AMO$ , we can see that $(7\sqrt{3})^2+7^2-2(7\sqrt{3})(7)\cos (\angle AMO)=361,$ so after simplification we get that $\cos (\theta +90)=-\frac{55\sqrt{3}}{98}$ . Then by trigonometric identities this simplifies to $\sin \theta =\frac{55\sqrt{3}}{98}$ . Applying the definition $\cos^2\theta +\sin^2\theta =1$ gives us that $\cos \theta =\frac{23}{98}$ . Applying the Law of Cosines again in $\triangle KMO$ , we get that $49+49-2\cdot 7\cdot 7\cdot \cos \theta =98-98\cdot \frac{23}{98}=98-23=75=KO^2,$ which tells us that $KO=5\sqrt{3}$ . The Pythagorean Theorem in $\triangle KOL$ gives that $OL=11$ , so the area of $\triangle KOL$ is $\frac{55\sqrt{3}}{2}$ . The rhombus $KL'K'L$ consists of four of these triangles, so its area is $4\cdot \frac{55\sqrt{3}}{2}=110\sqrt{3}$ .

Finally, the area of hexagon $BL'K'CLK$ is $49\sqrt{3}+110\sqrt{3}+49\sqrt{3}=208\sqrt{3}$ , and since this consists of quadrilaterals $BKLC$ and $CK'L'B$ which must be congruent by that rotation, the area of $BKLC$ is $104\sqrt{3}$ . Therefore the answer is $\boxed{104}$ .

~ethanzhang1001

Solution 3 (coordinates and bashy algebra)

By drawing our the triangle, I set A to be (0, 0) in the coordinate plane. I set C to be (x, 0) and B to be (0, y). I set K to be (a, b) and L to be (c, d). Then, since all of these distances are 14, I used coordinate geometry to set up the following equations: $a^{2}$ + $b^{2}$ = 196; $a^{2}$ + $(b - y)^{2}$ = 196; $(a - c)^{2}$ + $(b - d)^{2}$ = 196; $c^{2}$ + $d^{2}$ = 196; $(c - x)^{2}$ + $d^{2}$ . = 196. Notice by merging the first two equations, the only possible way for it to work is if $b - y$ = $-b$ which means $y = 2b$ . Next, since the triangle is right, and we know one leg is $2b$ as $y = 2b$ , the other leg, x, is $\sqrt{38^{2} - (2b)^{2}}$ .Then, plugging these in, we get a system of equations with 4 variables and 4 equations and solving, we get a = 2, b = 8 $\sqrt{3}$ , c = 13, d = 3 $\sqrt{3}$ . Now plugging in all the points and using the Pythagorean Theorem, we get the coordinates of the quadrilateral. By Shoelace, our area is 104 $\sqrt{3}$ . Thus, the answer is $\boxed{104}$ .

~ilikemath247365

Solution 4 (Trigonometry)

$[asy] import math; import geometry; import olympiad; point A,B,C,L,K; A=(0,0); C=(16sqrt(3),0); B=(0,26); L=(8sqrt(3),2); K=(3sqrt(3),13); draw(A--B--C--cycle); draw(A--K--L--cycle); draw(B--K); draw(C--L); draw(B--L); label("A",A,SW); label("B",B,NW); label("C",C,SE); label("K",K,W); label("L",L,NE); markscalefactor=1; draw(anglemark(L,C,A)); draw(anglemark(A,B,K)); [/asy]$ Immediately we should see that $\triangle{AKL}$ is equilateral, so $\angle{KAL}=60$ .

We assume $\angle{LCA}=x$ , and it is easily derived that $\angle{KBA}=30-x$ . Using trigonometry, we can say that $AC=28\cos{x}$ and $AB=28\cos{(30-x)}$ . Pythagoras tells us that $BC^2=AC^2+AB^2$ so now we evaluate as follows: \begin{align*} 38^2 &=28^2(\cos^2{x}+\cos^2{(30-x)}) \\ (\frac{19}{14})^2 &=\cos^2{x}+(\frac{\sqrt{3}}{2} \cos{x} - \frac{1}{2} \sin{x})^2 \\ &=\cos^2{x}+\frac{3}{4} \cos^2{x}-\frac{\sqrt{3}}{2}\sin{x} \cos{x}+\frac{1}{4}\sin^2{x} \\ &=\frac{3}{2} \cos^2{x}-\frac{\sqrt{3}}{2}\sin{x} \cos{x}+\frac{1}{4} \\ &=\frac{3}{4}(2\cos^2{x}-1)-\frac{\sqrt{3}}{4} (2\sin{x} \cos{x})+1 \\ (\frac{33}{14})(\frac{5}{14})&=\frac{\sqrt{3}}{2}(\frac{\sqrt{3}}{2}(\cos{2x})-\frac{1}{2} (\sin{2x})) \\ \frac{55\sqrt{3}}{98}&=\cos{(30-2x)} \\ \end{align*}

It is obvious that $\angle{ALC}=180-2x$ . We can easily derive $\cos{(150+(30-2x))}$ using angle addition we know, and then using cosine rule to find side $AC$ .

\begin{align*} \frac{55\sqrt{3}}{98}=\cos{(30-2x)} \\ \sin{(30-2x)}=\sqrt{1-\cos^2{(30-2x)}}=\frac{23}{98} \\ \cos{(180-2x)}=(-\frac{\sqrt{3}}{2})(\frac{55\sqrt{3}}{98})-(\frac{1}{2})(\frac{23}{98}) \\ \cos{(180-2x)}=-\frac{47}{49} \\ AC^2=14^2+14^2+2\cdot 14\cdot 14\cdot (\frac{47}{49}) \\ AC=\sqrt{768}=16\sqrt3 \\ \end{align*}

We easily find $\cos{x}=\frac{4\sqrt{3}}{7}$ and $\sin{x}=\frac{1}{7}$ (draw a perpendicular down from $L$ to $AC$ ). What we are trying to find is the area of $BKLC$ , which can be found by adding the areas of $\triangle{BKL}$ and $\triangle{BLC}$ . It is trivial that $\triangle{BKL}$ and $\triangle{ACL}$ are congruent, so we know that $BL=28\cos{x}$ . What we require is

\begin{align*} \frac{1}{2}(14)(14)(\sin{(180-2x)})+\frac{1}{2}(14)(28\cos{x})(\sin{(120+x)}) \\ \end{align*}

We do similar calculations to obtain that $\sin{(120+x)}=\frac{11}{14}$ and $\cos{(180-2x)}=-\frac{47}{49}$ implies $\sin{(180-2x)}=\frac{8\sqrt{3}}{49}$ , so now we plug in everything we know to calculate the area of the quadrilateral:

\begin{align*} & \frac{1}{2}(14)(14)(\sin{(180-2x)})+\frac{1}{2}(14)(28\cos{x})(\sin{(120+x)}) \\ &=\frac{1}{2}(14)(14)(\frac{8\sqrt{3}}{49})+\frac{1}{2}(14)(16\sqrt{3})(\frac{11}{14}) \\ &=16\sqrt{3}+88\sqrt{3} \\ &=104\sqrt{3} \\ \end{align*}

We see that $n=\boxed{104}$ .

~ lisztepos

~ Edited by Aoum

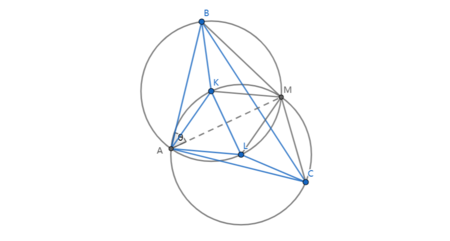
Solution 5 (Circles and Trigonometry)

Since $KB=KL=KA=14$ and $LK=LA=LC=14$ , we can construct 2 circles of radus 14 with $K$ and $L$ as the center of the two circles. Let the intersection of the 2 circles other than $A$ be point $M$ . Connect $BM$ , $CM$ , $KM$ , and $LM$ . Connect $AM$ , which is the radical axis of the 2 circles.

From the figure, we know that $[KLCB] = [KLCMB] - [BMC]$ $[KLCB] = [BKM] + [CLM] + [KLM] - [BMC]$

Let $\angle{BAM} = \theta$ , which means that $\angle{CAM} = \frac{\pi}{2} - \theta$ . For easier calculation, we temporarily define the radius of the 2 circles (which is 14) to be $R$ . $\angle{BAM}$ is an inscribed angle and $\angle{BKM}$ is a central angle, so $\angle{BKM} = 2\angle{BAM} = 2\theta$ . Similar with the other side, $\angle{CLM} = \pi-2\theta$ . $KM = KL = LM = R$ , so $\triangle{BKM}$ is an equilateral triangle.

Using the Law of Cosines, we get the area of each little triangle. $[BKM] = \frac{1}{2}\cdot R^2\cdot\sin(2\theta)$ $[CLM] = \frac{1}{2}\cdot R^2\cdot\sin(\pi-2\theta) = \frac{1}{2}\cdot R^2\cdot\sin(2\theta)$ $[KLM] = \frac{1}{2}\cdot\sin({\frac{\pi}{3}})=\frac{\sqrt3}{4}R^2$ \begin{align*} [BMC] & = \frac{1}{2}\cdot|BM|\cdot|MC|\cdot\sin({\frac{5\pi}{6}})\\ &= \frac{1}{2}\cdot\frac{1}{2}\cdot2R\sin(\theta)\cdot2R\sin(\frac{\pi}{2}-\theta)\\ &= R^2\cdot\sin(\theta)\cos(\theta)\\ &= \frac{1}{2}\cdot R^2\sin(2\theta)\\ \end{align*}

We can conclude that $[KLCB] = \frac{1}{2}\cdot R^2\cdot\sin(2\theta)+\frac{1}{2}\cdot R^2\cdot\sin(2\theta)+\frac{\sqrt3}{4}R^2-\frac{1}{2}\cdot R^2\sin(2\theta)$ $[KLCB] = {14}^2\cdot(\frac{\sin(2\theta)}{2}+\frac{\sqrt3}{4})$

Now, we just needed to find the value of $\sin(2\theta)$ . We analyze the $\triangle{BMC}$ . We already know that $\angle{BMC} = {150}^{\circ}$ and $BM = 2R\sin(\theta)$ and $BM = 2R\cos(\theta)$ . Using the Laws of Cosines (again!) and the given condition of $BC = 38$ , we can create a formula on $\theta$ .

${BC}^2 = {BM}^2+{CM}^2-2\cdot BM\cdot MC\cdot\cos(\angle{BMC})$ ${BC}^2 = (2R\sin(\theta))^2+(2R\cos(\theta))^2-2\cdot\cos({150}^{\circ})\cdot(2R\cos(\theta))\cdot(2R\cos(\theta)) = {38}^2$ $4R^2(\sin^2(\theta)+\cos^2(\theta)+\sqrt3\sin(\theta)\cos(\theta)) = {38}^2$ $4R^2(1+\frac{\sqrt3}{2}\cdot\sin(2\theta)) = {38}^2$ $4R^2+\frac{4R^2\sqrt3}{2}\cdot\sin(2\theta)) = {38}^2$ $\sin(2\theta) = \frac{2}{\sqrt3}\cdot(\frac{{38}^2}{4\cdot{38}^2}-1)$ $\sin(2\theta) = \frac{2\cdot165}{\sqrt3\cdot{14}^2} = \frac{165}{98\sqrt3}$

We put the calculated value of $\sin(2\theta)$ back into $[KLCB]$ : $[KLCB] = {14}^2\cdot(\frac{165}{2\cdot98\sqrt3}+\frac{\sqrt3}{4})$ $[KLCB] = 55\sqrt3+49\sqrt3 = 104\sqrt3$

Therefore, $n=\boxed{104}$ .

~cassphe

Solution 6 (Trig Identities; warning: bashy)

Consider a diagram to the original problem (credit to solution 4):

$[asy] import math; import geometry; import olympiad; point A,B,C,L,K; A=(0,0); C=(16sqrt(3),0); B=(0,26); L=(8sqrt(3),2); K=(3sqrt(3),13); draw(A--B--C--cycle); draw(A--K--L--cycle); draw(B--K); draw(C--L); draw(B--L); label("A",A,SW); label("B",B,NW); label("C",C,SE); label("K",K,W); label("L",L,NE); markscalefactor=1; [/asy]$

Now, let us simplify the problem further. We know that $K$ and $L$ must lie on the perpendicular bisectors of $AB$ and $AC$ , respectively. The real problem here is the equilateral triangle in the middle, inscribed in a rectangle with diagonal length 18.

We create a further simplified problem: given that the inscribed equilateral triangle of a certain rectangle with diagonal length $19$ has side length $14$ , find the sides and intersection points on this rectangle. For reference, here is a diagram:

$[asy] import math; import geometry; import olympiad; point A,B,C,D,L,K; A=(0,0); D=(13,0); B=(0,8sqrt(3)); C=(13,8sqrt(3)); L=(13,3sqrt(3)); K=(2,8sqrt(3)); draw(A--B--C--D--cycle); draw(A--K--L--cycle); label("A",A,SW); label("B",B,NW); label("C",C,NE); label("K",K,N); label("L",L,E); label("D",D,SE); markscalefactor=1; [/asy]$

Note the angles $\angle{LAD}$ and $\angle{BAK}$ . Since $\angle{LAD} + \angle{BAK} + 60^{\circ} = 90^{\circ}$ , $\angle{LAD} + \angle{BAK} = 30^{\circ}$ , and $\angle{BAK} = 30^{\circ} - \angle{LAD}$ . Thus, let $\angle{LAD} = \alpha$ and $\angle{BAK} = 30 - \alpha$ .

Now, we know that $AB^2 + AD^2 = 19^2$ , as the hypotenuse of the larger right triangle is $38$ . However, we can also express AB and AB in terms of $\alpha$ : $AB = 14(\cos(30^{\circ}-\alpha))$ and $AD = 14(\cos(\alpha))$ . Thus, $\cos^2(\alpha) + \cos^2(30^{\circ}-\alpha) = 361/196$ . We expand this using the cosine difference identity:

$\cos^2(\alpha) + (\cos(30^{\circ})\cos(\alpha) + \sin(30^{\circ})\sin(\alpha))^2 = \frac{361}{196}$

$\frac{7}{4}\cos^2(\alpha) + \frac{1}{4}\sin^2(\alpha) + \frac{\sqrt3}{2}\sin(\alpha)\cos(\alpha) = \frac{361}{196}$

Using the fact that $\sin^2(\alpha) + \cos^2(\alpha) = 1$ , then multiplying the entire equation by $2$ ,

$3\cos^2(\alpha) + \sqrt3\sin(\alpha)\cos(\alpha) = \frac{156}{49}$

Now, to save some writing, let us denote $\sin(\alpha)$ with $x$ , and $\cos(\alpha)$ with $y$ .

We have the following equations:

$x^2 + y^2 = 1$

$3y^2 + \sqrt3xy = \frac{156}{49}$

Substituting $x$ for $y$ , moving $3y^2$ to the left side, squaring, and dividing by 9, we end up with the quartic:

$\frac{4}{3}y^4 - \frac{361}{147}y^2 + \frac{52^2}{49^2} = 0$

Using the quadratic formula, we end up with this:

$y^2 = \frac{\frac{361}{49} \pm \frac{1}{49}\cdot\sqrt{361^2 - 208^2\cdot3}}{8}$

Now, we could just compute $361^2 - 208^2\cdot3$ , but instead, we can do this:

$361^2 - 208^2\cdot3 = (129600 + 720 + 1) - (40000 + 3200 + 64)\cdot3$

$(129600 + 721) - (43200 + 64)\cdot3$

$(129600 + 721) - (129600 + 192) = 529 = 23^2$

Thus, we have two cases:

$1. \cos(\alpha) = \frac{13}{14}$

$2. \cos(\alpha) = \frac{4\sqrt3}{7}$

Both lead to the same side lengths of the rectangle: $8\sqrt3$ , and $13$ . Referring back to our original rectangle diagram and plugging in our trigonometric values, we get that $CK = 13 - 2 = 11$ , and $CL = 8\sqrt3 - 3\sqrt3 = 5\sqrt3$ . Thus, the area of the original quadrilateral is $\frac{88\sqrt3 + 55\sqrt3 + 65\sqrt3}{2}$ , or $\boxed{104}\sqrt3$ .

~Stead

Remarks

This problem can be approached either by analytic geometry or by trigonometric manipulation. The characteristics of this problem make it highly similar to 2017 AIME I Problem 15 (Link).

~Bloggish

2025 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 13	Followed by Problem 15
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search