2016 IMO Problems/Problem 1
Contents
Problem
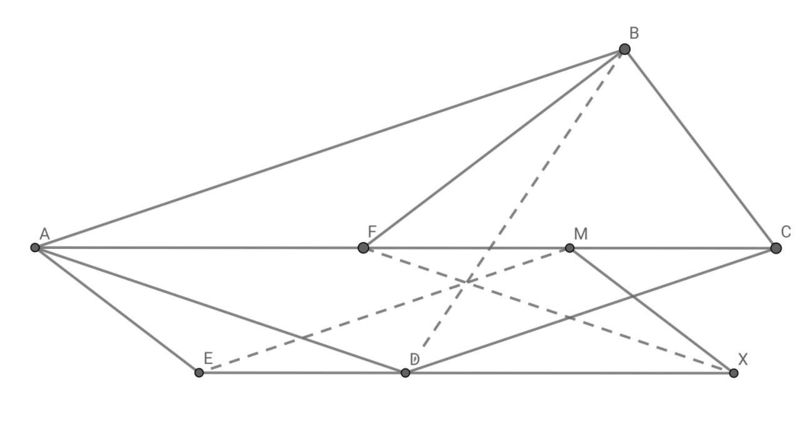
Triangle ![]() has a right angle at
has a right angle at ![]() . Let
. Let ![]() be the point on line
be the point on line ![]() such that
such that ![]() and
and ![]() lies between
lies between ![]() and
and ![]() . Point
. Point ![]() is chosen so that
is chosen so that ![]() and
and ![]() is the bisector of
is the bisector of ![]() . Point
. Point ![]() is chosen so that
is chosen so that ![]() and
and ![]() is the bisector of
is the bisector of ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() . Let
. Let ![]() be the point such that
be the point such that ![]() is a parallelogram. Prove that
is a parallelogram. Prove that ![]() and
and ![]() are concurrent.
are concurrent.
Solution
The Problem shows that \(\angle DAC = \angle DCA = \angle CAD\), it follows that \(AB \parallel CD\). Extend \(DC\) to intersect \(AB\) at \(G\), we get \(\angle GFA = \angle GFB = \angle CFD\). Making triangles \(\triangle CDF\) and \(\triangle AGF\) similar. Also, \(\angle FDC = \angle FGA = 90^\circ\) and \(\angle FBC = 90^\circ\), which points \(D\), \(C\), \(B\), and \(F\) are concyclic.
And \(\angle BFC = \angle FBA + \angle FAB = \angle FAE = \angle AFE\). Triangle \(\triangle AFE\) is congruent to \(\triangle FBM\), and \(AE = EF = FM = MB\). Let \(MX = EA = MF\), then points \(B\), \(C\), \(D\), \(F\), and \(X\) are concyclic.
Finally \(AD = DB\) and \(\angle DAF = \angle DBF = \angle FXD\). \(\angle MFX = \angle FXD = \angle FXM\) and \(FE \parallel MD\) with \(EF = FM = MD = DE\), making \(EFMD\) a rhombus. And \(\angle FBD = \angle MBD = \angle MXF = \angle DXF\) and triangle \(\triangle BEM\) is congruent to \(\triangle XEM\), while \(\triangle MFX\) is congruent to \(\triangle MBD\) which is congruent to \(\triangle FEM\), so \(EM = FX = BD\).
Solution 2
Let ![]() . And WLOG,
. And WLOG, ![]() . Hence,
. Hence, ![]() ,
,
![]()
![]() ,
,
![]()
![]() and
and
![]()
![]() .
.
So ![]() which means
which means ![]() ,
, ![]() ,
, ![]() and
and ![]() are concyclic. We know that
are concyclic. We know that ![]() and
and ![]() , so we conclude
, so we conclude ![]() is parallelogram. So
is parallelogram. So ![]() . That means
. That means ![]() is isosceles trapezoid. Hence,
is isosceles trapezoid. Hence, ![]() . By basic angle chasing,
. By basic angle chasing,
![]() and
and ![]() and we have seen that
and we have seen that ![]() , so
, so ![]() is isosceles trapezoid. And we know that
is isosceles trapezoid. And we know that ![]() bisects
bisects ![]() , so
, so ![]() is the symmetrical axis of
is the symmetrical axis of ![]() .
.
![]() and
and ![]() ,
, ![]() and
and ![]() are symmetrical respect to
are symmetrical respect to ![]() . Hence, the symmetry of
. Hence, the symmetry of ![]() with respect to
with respect to ![]() is
is ![]() . And we are done
. And we are done ![]() .
.
~EgeSaribas
See Also
| 2016 IMO (Problems) • Resources | ||
| Preceded by First Problem |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 2 |
| All IMO Problems and Solutions | ||