2016 AIME I Problems/Problem 6

Problem

In $\triangle ABC$ let $I$ be the center of the inscribed circle, and let the bisector of $\angle ACB$ intersect $AB$ at $L$ . The line through $C$ and $L$ intersects the circumscribed circle of $\triangle ABC$ at the two points $C$ and $D$ . If $LI=2$ and $LD=3$ , then $IC=\tfrac{m}{n}$ , where $m$ and $n$ are relatively prime positive integers. Find $m+n$ .

Solution 1

Suppose we label the angles as shown below. $[asy] size(150); import olympiad; real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; pair A=(0,0),B=(c,0),D=(c/2,-sqrt(25-(c/2)^2)); pair C=intersectionpoints(circle(A,b),circle(B,a))[0]; pair I=incenter(A,B,C); pair L=extension(C,D,A,B); dot(I^^A^^B^^C^^D); draw(C--D); path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} draw(A--B--D--cycle); draw(circumcircle(A,B,D)); draw(A--C--B); draw(A--I--B^^C--I); draw(incircle(A,B,C)); label("$A$",A,SW,fontsize(8)); label("$B$",B,SE,fontsize(8)); label("$C$",C,N,fontsize(8)); label("$D$",D,S,fontsize(8)); label("$I$",I,NE,fontsize(8)); label("$L$",L,SW,fontsize(8)); label("$\alpha$",A,5*dir(midangle(C,A,I)),fontsize(8)); label("$\alpha$",A,5*dir(midangle(I,A,B)),fontsize(8)); label("$\beta$",B,12*dir(midangle(A,B,I)),fontsize(8)); label("$\beta$",B,12*dir(midangle(I,B,C)),fontsize(8)); label("$\gamma$",C,5*dir(midangle(A,C,I)),fontsize(8)); label("$\gamma$",C,5*dir(midangle(I,C,B)),fontsize(8)); [/asy]$ As $\angle BCD$ and $\angle BAD$ intercept the same arc, we know that $\angle BAD=\gamma$ . Similarly, $\angle ABD=\gamma$ . Also, using $\triangle ICA$ , we find $\angle CIA=180-\alpha-\gamma$ . Therefore, $\angle AID=\alpha+\gamma$ . Therefore, $\angle DAI=\angle AID=\alpha+\gamma$ , so $\triangle AID$ must be isosceles with $AD=ID=5$ . Similarly, $BD=ID=5$ . Then $\triangle DLB \sim \triangle ALC$ , hence $\frac{AL}{AC} = \frac{3}{5}$ . Also, $AI$ bisects $\angle LAC$ , so by the Angle Bisector Theorem $\frac{CI}{IL} =\frac{AC}{AL}= \frac{5}{3}$ . Thus $CI = \frac{10}{3}$ , and the answer is $\boxed{013}$ .

Solution 2 (Incenter/Excenter)

See the diagram in Solution 1.

Let $\Delta ABC$ 's $C$ -excenter be $J_C$ . Since $CI$ is an angle bisector, $\angle ACD = \angle BCD$ , meaning that $D$ is the midpoint of arc $\overarc{BC}$ . By the Incenter/Excenter Lemma, $DA=DI=DB=DJ_C=2+3=5$ , and applying Power of a Point on circle $D$ gives $AL\cdot AB = LI\cdot LJ_C = 2(3+5) = 16$ . Applying Power of a Point again on $\Delta ABC$ 's circumcircle gives $AL\cdot LB = LC\cdot LD = 16$ , and since $LD = 3$ , $LC = \frac{16}{3}$ . Thus $IC = LC-LI = \frac{16}{3}-2 = \frac{10}{3}$ . We submit $10+3=\boxed{013}$ . - NamelyOrange

Solution 3

WLOG assume $\triangle ABC$ is isosceles. Then, $L$ is the midpoint of $AB$ , and $\angle CLB=\angle CLA=90^\circ$ . Draw the perpendicular from $I$ to $CB$ , and let it meet $CB$ at $E$ . Since $IL=2$ , $IE$ is also $2$ (they are both inradii). Set $BD$ as $x$ . Then, triangles $BLD$ and $CEI$ are similar, and $\tfrac{2}{3}=\tfrac{CI}{x}$ . Thus, $CI=\tfrac{2x}{3}$ . $\triangle CBD \sim \triangle CEI$ , so $\tfrac{IE}{DB}=\tfrac{CI}{CD}$ . Thus $\tfrac{2}{x}=\tfrac{(2x/3)}{(2x/3+5)}$ . Solving for $x$ , we have: $x^2-2x-15=0$ , or $x=5, -3$ . $x$ is positive, so $x=5$ . As a result, $CI=\tfrac{2x}{3}=\tfrac{10}{3}$ and the answer is $\boxed{013}$

Solution 4

WLOG assume $\triangle ABC$ is isosceles (with vertex $C$ ). Let $O$ be the center of the circumcircle, $R$ the circumradius, and $r$ the inradius. A simple sketch will reveal that $\triangle ABC$ must be obtuse (as an acute triangle will result in $LI$ being greater than $DL$ ) and that $O$ and $I$ are collinear. Next, if $OI=d$ , $DO+OI=R+d$ and $R+d=DL+LI=5$ . Euler gives us that $d^{2}=R(R-2r)$ , and in this case, $r=LI=2$ . Thus, $d=\sqrt{R^{2}-4R}$ . Solving for $d$ , we have $R+\sqrt{R^{2}-4R}=5$ , then $R^{2}-4R=25-10R+R^{2}$ , yielding $R=\frac{25}{6}$ . Next, $R+d=5$ so $d=\frac{5}{6}$ . Finally, $OC=OI+IC$ gives us $R=d+IC$ , and $IC=\frac{25}{6}-\frac{5}{6}=\frac{10}{3}$ . Our answer is then $\boxed{013}$ .

Solution 5

Since $\angle{LAD} = \angle{BDC}$ and $\angle{DLA}=\angle{DCB}$ , $\triangle{DLA}\sim\triangle{DBC}$ . Also, $\angle{DAC}=\angle{BLC}$ and $\angle{ACD}=\angle{LCB}$ so $\triangle{DAC}\sim\triangle{BLC}$ . Now we can call $AC$ , $b$ and $BC$ , $a$ . By angle bisector theorem, $\frac{AD}{DB}=\frac{AC}{BC}$ . So let $AD=bk$ and $DB=ak$ for some value of $k$ . Now call $IC=x$ . By the similar triangles we found earlier, $\frac{3}{ak}=\frac{bk}{x+2}$ and $\frac{b}{x+5}=\frac{x+2}{a}$ . We can simplify this to $abk^2=3x+6$ and $ab=(x+5)(x+2)$ . So we can plug the $ab$ into the first equation and get $(x+5)(x+2)k^2=3(x+2) \rightarrow k^2(x+5)=3$ . We can now draw a line through $A$ and $I$ that intersects $BC$ at $E$ . By mass points, we can assign a mass of $a$ to $A$ , $b$ to $B$ , and $a+b$ to $D$ . We can also assign a mass of $(a+b)k$ to $C$ by angle bisector theorem. So the ratio of $\frac{DI}{IC}=\frac{(a+b)k}{a+b}=k=\frac{2}{x}$ . So since $k=\frac{2}{x}$ , we can plug this back into the original equation to get $\left(\frac{2}{x}\right)^2(x+5)=3$ . This means that $\frac{3x^2}{4}-x-5=0$ which has roots -2 and $\frac{10}{3}$ which means our $CI=\frac{10}{3}$ and our answer is $\boxed{013}$ .

Solution 6

Since $\angle BCD$ and $\angle BAD$ both intercept arc $BD$ , it follows that $\angle BAD=\gamma$ . Note that $\angle AID=\alpha+\gamma$ by the external angle theorem. It follows that $\angle DAI=\angle AID=\alpha+\gamma$ , so we must have that $\triangle AID$ is isosceles, yielding $AD=ID=5$ . Note that $\triangle DLA \sim \triangle DAC$ , so $\frac{DA}{DL} = \frac{DC}{DA}$ . This yields $DC = \frac{25}{3}$ . It follows that $CI = DC - DI = \frac{10}{3}$ , giving a final answer of $\boxed{013}$ .

Solution 7

Let $I_C$ be the excenter opposite to $C$ in $ABC$ . By the incenter-excenter lemma $DI=DC \therefore$ $LI_C=8,LI=2,II_C=10$ . Its well known that $(I_C,I,L,C)=-1 \implies \dfrac{LI_C}{LI}.\dfrac{CI}{CI_C}=-1 \implies \dfrac{CI}{CI+10}=\dfrac{1}{4} \implies \boxed{CI=\dfrac{10}{3}}$ . $\blacksquare$ ~Pluto1708

Alternate solution: We can use the angle bisector theorem on $\triangle CBL$ and bisector $BI$ to get that $\tfrac{CI}{IL}=\tfrac{CI}{2}=\tfrac{BC}{BL}$ . Since $\triangle CBL \sim \triangle ADL$ , we get $\tfrac{BC}{BL}=\tfrac{AD}{DL}=\tfrac{5}{3}$ . Thus, $CI=\tfrac{10}{3}$ and $p+q=\boxed{13}$ . (https://artofproblemsolving.com/community/c759169h1918283_geometry_problem)

Solution 8

We can just say that quadrilateral $ADBC$ is a right kite with right angles at $A$ and $B$ . Let us construct another similar right kite with the points of tangency on $AC$ and $BC$ called $E$ and $F$ respectively, point $I$ , and point $C$ . Note that we only have to look at one half of the circle since the diagram is symmetrical. Let us call $CI$ $x$ for simplicity's sake. Based on the fact that $\triangle BCD$ is similar to $\triangle FCI$ we can use triangle proportionality to say that $BD$ is $2\frac{x+5}{x}$ . Using geometric mean theorem we can show that $BL$ must be $\sqrt{3x+6}$ . With Pythagorean Theorem we can say that $3x+6+9=4{(\frac{x+5}{x})}^2$ . Multiplying both sides by $x^2$ and moving everything to LHS will give you $3{x}^3+11{x}^2-40x-100=0$ Since $x$ must be in the form $\frac{p}{q}$ we can assume that $x$ is most likely a positive fraction in the form $\frac{p}{3}$ where $p$ is a factor of $100$ . Testing the factors in synthetic division would lead $x = \frac{10}{3}$ , giving us our desired answer $\boxed{013}$ . ~Lopkiloinm

Solution 9 (Cyclic Quadrilaterals)

$[asy] size(150); import olympiad; real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; pair A=(0,0),B=(c,0),D=(c/2,-sqrt(25-(c/2)^2)); pair C=intersectionpoints(circle(A,b),circle(B,a))[0]; pair I=incenter(A,B,C); pair L=extension(C,D,A,B); dot(I^^A^^B^^C^^D); draw(C--D); path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} draw(A--B--D--cycle); draw(circumcircle(A,B,D)); draw(A--C--B); draw(A--I--B^^C--I); draw(incircle(A,B,C)); label("$A$",A,SW,fontsize(8)); label("$B$",B,SE,fontsize(8)); label("$C$",C,N,fontsize(8)); label("$D$",D,S,fontsize(8)); label("$I$",I,NE,fontsize(8)); label("$L$",L,SW,fontsize(8)); label("$\alpha$",A,5*dir(midangle(C,A,I)),fontsize(8)); label("$\alpha$",A,5*dir(midangle(I,A,B)),fontsize(8)); label("$\beta$",B,12*dir(midangle(A,B,I)),fontsize(8)); label("$\beta$",B,12*dir(midangle(I,B,C)),fontsize(8)); label("$\gamma$",C,5*dir(midangle(A,C,I)),fontsize(8)); label("$\gamma$",C,5*dir(midangle(I,C,B)),fontsize(8)); [/asy]$ Connect $D$ to $A$ and $D$ to $B$ to form quadrilateral $ACBD$ . Since quadrilateral $ACBD$ is cyclic, we can apply Ptolemy's Theorem on the quadrilateral.

Denote the length of $BD$ and $AD$ as $z$ (they must be congruent, as $\angle ABD$ and $\angle DAB$ are both inscribed in arcs that have the same degree measure due to the angle bisector intersecting the circumcircle at $D$ ), and the lengths of $BC$ , $AC$ , $AB$ , and $CI$ as $a,b,c, x$ , respectively.

After applying Ptolemy's, one will get that:

$z(a+b)=c(x+5)$

Next, since $ACBD$ is cyclic, triangles $ALD$ and $CLB$ are similar, yielding the following equation once simplifications are made to the equation $\frac{AD}{CB}=\frac{AL}{BL}$ , with the length of $BL$ written in terms of $a,b,c$ using the angle bisector theorem on triangle $ABC$ :

$zc=3(a+b)$

Next, drawing in the bisector of $\angle BAC$ to the incenter $I$ , and applying the angle bisector theorem, we have that:

$cx=2(a+b)$

Now, solving for $z$ in the second equation, and $x$ in the third equation and plugging them both back into the first equation, and making the substitution $w=\frac{a+b}{c}$ , we get the quadratic equation:

$3w^2-2w-5=0$

Solving, we get $w=5/3$ , which gives $z=5$ and $x=10/3$ , when we rewrite the above equations in terms of $w$ . Thus, our answer is $\boxed{013}$ and we're done.

-mathislife52

Solution 10(Visual)

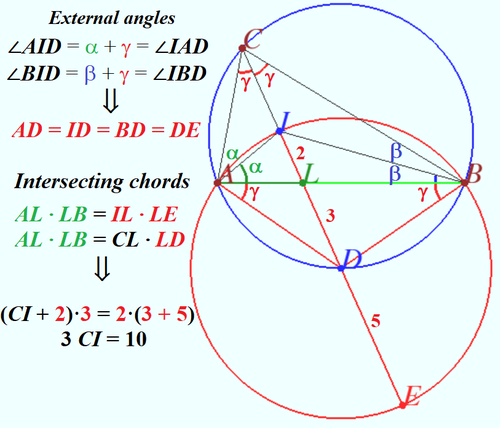vladimir.shelomovskii@gmail.com, vvsss

Solution 11

Let $AB=c,BC=a,CA=b$ , and $x=\tfrac{a+b}{c}$ . Then, notice that $\tfrac{CI}{IL}=\tfrac{a+b}{c}=x$ , so $CI=IL\cdot{}x=2x$ . Also, by the incenter-excenter lemma, $AD=BD=ID=IL+LD=5$ . Therefore, by Ptolemy's Theorem on cyclic quadrilateral $ABCD$ , $5a+5b=c(2x+5)$ , so $5\left(\tfrac{a+b}{c}\right)=2x+5$ , so $5x=2x+5$ . Solving, we get that $x=\tfrac{5}{3}$ , so $CI=\tfrac{10}{3}$ and the answer is $10+3=\boxed{013}$ .

Solution 12

Perform a $\sqrt{bc}$ Inversion followed by a reflection along the angle bisector of $\angle BCA$ .

It's well known that $AB \leftrightarrow \odot CBA \implies L \leftrightarrow D$ $I \leftrightarrow I_A$ where $I_A$ is the $A-$ excenter.

Also by Fact 5, $DI_A = 5$ .

So, $CL \cdot CD = CI \cdot CI_A$ $\implies (CI + IL) \cdot (CI + ID) = (CI) \cdot (CI + II_A)$ $\implies (CI + 2) \cdot (CI + 5) = (CI) \cdot (CI + 10)$ $\implies 7CI +10= 10CI$ $\implies CI = \boxed{\dfrac{10}{3}}.\blacksquare$

~kamatadu

Solution 13

Without loss of generality, let $\triangle ABC$ be isosceles. Note that by the incenter-excenter lemma, $DI = DA = DB.$ Hence, $DA=DB=5.$ Let the point of tangency of the incircle and $\overline{BC}$ be $F$ and the point of tangency of the incircle and $\overline{AC}$ be $E.$ We note that $\angle ALC = \angle BLC = 90^\circ$ and $LA=LB=4,$ which immediately gives $AE=BF=4.$ Applying the Pythagorean Theorem on $\triangle ALC$ and $\triangle IEC$ gives $2^2+x^2=y^2$ and $4^2+(2+y)^2 = (4+x)^2.$ Solving for $y$ gives us $y=\frac{10}{3}.$ Therefore, $IC = \frac{10}{3}$ so the answer is $\boxed{13}.$

~peelybonehead

Solution 14 (Trig)

Let $C_1\in AB$ be the point such that $IC_1\perp AB$ , and let $D_1\in AB$ be defined similarly for $D$ . We know that $\triangle IC_1L\sim\triangle DD_1L$ , so by triangle ratios $DD_1=\frac{3}{2}r$ , where $r$ is the inradius. Additionally, by cyclic quadrilaterals, we know that $\angle BAD=\angle DAB=\frac{\gamma}{2}$ , where $\gamma$ is equivalent to $\angle ACB$ . Thus $\triangle ADB$ is isosceles and $DD_1$ is the perpendicular bisector of the triangle, so $AD_1=\frac{c}{2}$ . Since $\tan\left(\frac{\gamma}{2}\right)=\sqrt{\frac{(s-a)(s-b)}{s(s-c)}}$ from formulas (where $s$ is half the perimeter of $\triangle ABC$ ) and since $\tan\left(\frac{\gamma}{2}\right)=\frac{\frac{3}{2}r}{\frac{1}{2}c}$ from $\triangle ADB$ , we can set up an equation:

$\sqrt{\frac{(s-a)(s-b)}{s(s-c)}}=\frac{\frac{3}{2}r}{\frac{1}{2}c}\implies\frac{\sqrt{s(s-a)(s-b)(s-c)}}{s(s-c)}=\frac{3rs}{cs}\implies\frac{[ABC]}{s(s-c)}=\frac{3[ABC]}{cs}$

$\implies\frac{1}{s-c}=\frac{3}{c}\implies \frac{s}{c}=\frac{4}{3}$

Let $C_2\in AB$ such that $CC_2\perp AB$ . Then $CC_2=\frac{2[ABC]}{c}$ . Using the area formula $[ABC]=rs$ and our fact from above yields $CC_2=\frac{8}{3}r$ . We then notice that $\triangle CC_2L\sim\triangle IC_1L$ , so if we let $x=CI$ , by triangle ratios we find that $\frac{\frac{8}{3}r}{x+2}=\frac{r}{2}$ , leading to $x=\frac{10}{3}$ . Thus the answer is $10+3=\boxed{013}$ .

~eevee9406

2016 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 5	Followed by Problem 7
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search