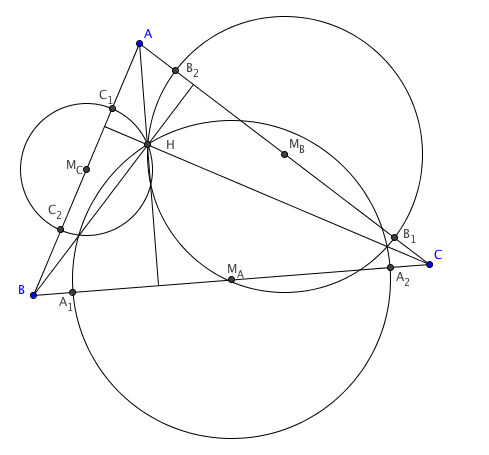
2008 IMO Problems/Problem 1
Problem
An acute-angled triangle ![]() has orthocentre
has orthocentre ![]() . The circle passing through
. The circle passing through ![]() with centre the midpoint of
with centre the midpoint of ![]() intersects the line
intersects the line ![]() at
at ![]() and
and ![]() . Similarly, the circle passing through
. Similarly, the circle passing through ![]() with centre the midpoint of
with centre the midpoint of ![]() intersects the line
intersects the line ![]() at
at ![]() and
and ![]() , and the circle passing through
, and the circle passing through ![]() with centre the midpoint of
with centre the midpoint of ![]() intersects the line
intersects the line ![]() at
at ![]() and
and ![]() . Show that
. Show that ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() lie on a circle.
lie on a circle.
Solution
Let ![]() ,
, ![]() , and
, and ![]() be the midpoints of sides
be the midpoints of sides ![]() ,
, ![]() , and
, and ![]() , respectively. It's not hard to see that
, respectively. It's not hard to see that ![]() . We also have that
. We also have that ![]() , so
, so ![]() . Now note that the radical axis of two circles is perpendicular to the line connecting their centers. We know that
. Now note that the radical axis of two circles is perpendicular to the line connecting their centers. We know that ![]() is on the radical axis of the circles centered at
is on the radical axis of the circles centered at ![]() and
and ![]() , so
, so ![]() is too. We then have
is too. We then have ![]() . This implies that
. This implies that ![]() , so
, so ![]() . Therefore
. Therefore ![]() . This shows that quadrilateral
. This shows that quadrilateral ![]() is cyclic. Note that the center of its circumcircle is at the intersection of the perpendicular bisectors of the segments
is cyclic. Note that the center of its circumcircle is at the intersection of the perpendicular bisectors of the segments ![]() and
and ![]() . However, these are just the perpendicular bisectors of
. However, these are just the perpendicular bisectors of ![]() and
and ![]() , which meet at the circumcenter of
, which meet at the circumcenter of ![]() , so the circumcenter of
, so the circumcenter of ![]() is the circumcenter of triangle
is the circumcenter of triangle ![]() . Similarly, the circumcenters of
. Similarly, the circumcenters of ![]() and
and ![]() are coincident with the circumcenter of
are coincident with the circumcenter of ![]() . The desired result follows.
. The desired result follows.
See Also
| 2008 IMO (Problems) • Resources | ||
| Preceded by First Problem |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 2 |
| All IMO Problems and Solutions | ||