Squeeze Theorem
The Squeeze Theorem (also called the Sandwich Theorem or the Squeeze Play Theorem) is a relatively simple theorem that deals with calculus, specifically limits.
Theorem
Suppose 
is between 
and 
for all 
in a neighborhood of the point 
. If 
and 
approach some common limit 
as approaches , then 
.
Proof
If is between and for all in the neighborhood of , then either 
or 
for all in this neighborhood. The two cases are the same up to renaming our functions, so assume without loss of generality that .
We must show that for all 
there is some 
for which 
implies 
.
Now since 
, there must exist 
such that
![\[|x-S|<\delta_1 \Rightarrow |g(x)-L|<\varepsilon \textrm{ and } |x-S|<\delta_2 \Rightarrow |h(x)-L|<\varepsilon.\]](http://latex.artofproblemsolving.com/9/c/0/9c0b9eee7b3368e1fef612e618fbe1fc05954332.png)
Now let 
. If then
So . Now by the definition of a limit we get as desired.
Applications and examples
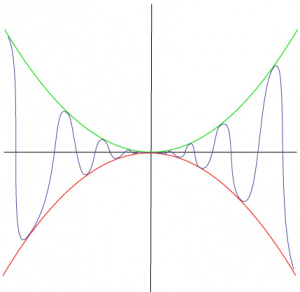
The Squeeze Theorem can be used to evaluate limits that might not normally be defined. An example is the function 
with thelimit $\lim_{x\to\0} f(x)=x^2 e^{\sin\frac{1}{x}}$ (Error compiling LaTeX. Unknown error_msg). The limit is not normally defined, because the function oscillates infinitely many times around 0, but it can be evaluated with the Squeeze Theorem as following. Create two functions, 
and 
. It is easy to see that around 0, the function in question is squeezed between these two functions, and the limit as both of these approach 0 is 0, so $\lim_{x\to\0} x^2 e^{\sin\frac{1}{x}}$ (Error compiling LaTeX. Unknown error_msg) is 0.
