1988 AIME Problems/Problem 7
Problem
In triangle 
, 
, and the altitude from 
divides 
into segments of length 3 and 17. What is the area of triangle ?
Solution
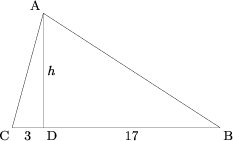
Let 
be the intersection of the altitude with 
, and 
be the length of the altitude. Without loss of generality, let 
and 
. Then 
and 
. Using the tangent sum formula,
$\begin{eqnarray*} \tan CAB &=& \tan (DAB + CAD)\\ \frac{22}{7} &=& \frac{\tan DAB + \tan CAD}{1 - \tan DAB \cdot \tan CAD} \\ &=& \frac{\frac{17}{h} + \frac{3}{h}}{1 - \left(\frac{17}{h}\right)\left(\frac{3}{h}\right)} \\ \frac{22}{7} &=& \frac{20h}{h^2 - 51}\\ 0 &=& 22h^2 - 140h - 22 \cdot 51\\ 0 &=& (11h + 51)(h - 11)
\end{eqnarray*}$ (Error compiling LaTeX. Unknown error_msg)The postive value of 
, so the area is 
.
See also
| 1988 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 6 |
Followed by Problem 8 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
