2011 AIME II Problems/Problem 8
Problem
Let ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() be the 12 zeroes of the polynomial
be the 12 zeroes of the polynomial ![]() . For each
. For each ![]() , let
, let ![]() be one of
be one of ![]() or
or ![]() . Then the maximum possible value of the real part of
. Then the maximum possible value of the real part of ![]() can be written as
can be written as ![]() , where
, where ![]() and
and ![]() are positive integers. Find
are positive integers. Find ![]() .
.
Solution
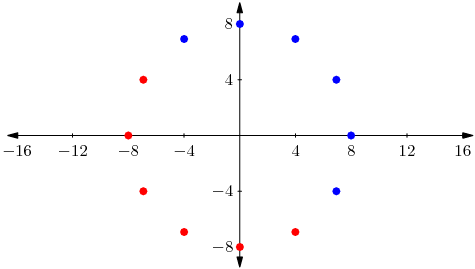
The twelve dots above represent the 12 roots of the equation ![]() . If we write
. If we write ![]() , then the real part of
, then the real part of ![]() is
is ![]() and the real part of
and the real part of ![]() is
is ![]() . The blue dots represent those roots
. The blue dots represent those roots ![]() for which the real part of
for which the real part of ![]() is greater than the real part of
is greater than the real part of ![]() , and the red dots represent those roots
, and the red dots represent those roots ![]() for which the real part of
for which the real part of ![]() is greater than the real part of
is greater than the real part of ![]() . Now, the sum of the real parts of the blue dots is easily seen to be
. Now, the sum of the real parts of the blue dots is easily seen to be ![]() and the negative of the sum of the imaginary parts of the red dots is easily seen to also be
and the negative of the sum of the imaginary parts of the red dots is easily seen to also be ![]() . Hence our desired sum is
. Hence our desired sum is ![]() , giving the answer
, giving the answer ![]() .
.
See also
| 2011 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 7 |
Followed by Problem 9 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()









