2012 AMC 10B Problems/Problem 14
Revision as of 22:21, 26 February 2012 by Jm314 (talk | contribs) (Created page with "==Solution== File:2012_AMC-10B-14.jpg Observe that the rhombus is made up of two congruent equilateral triangles with side length equal to GF. Since AE has length sqrt(3)...")
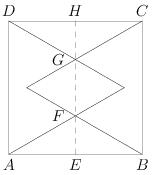
Solution
Observe that the rhombus is made up of two congruent equilateral triangles with side length equal to GF. Since AE has length sqrt(3) and triangle AEF is a 30-60-90 triangle, it follows that EF has length 1. By symmetry, HG also has length 1. Thus GF has length 2sqrt(3) - 2. The formula for the area of an equilateral triangle of length s is (s^2)sqrt(3)/4. It follows that the area of the rhombus is:
2((2sqrt(3) - 2)^2)sqrt(3)/4 = (sqrt(3)/2)(16 - 8sqrt(3)) = 8sqrt(3)-12. Thus, answer choice D is correct.