Trigonometry

Trigonometry seeks to find the lengths of a triangle's sides, given 2 angles and a side. Trigonometry is closely related to analytic geometry.

Basic definitions

Usually we call an angle $\displaystyle \theta$ , read "theta", but $\theta$ is just a variable. We could just as well call it $a$ .

For the following definitions, the "opposite side" is the side opposite of angle $\displaystyle \theta$ and the "adjacent side" is the side that is part of angle $\displaystyle \theta$ but is not the hypotenuse.

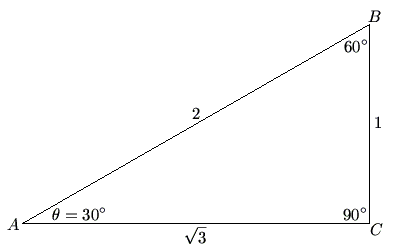
i.e. If ABC is a right triangle with right angle C, and angle A = $\displaystyle \theta$ , then BC is the "opposite side", AC is the "adjacent side", and AB is the hypotenuse.

Sine

The sine of an angle $\theta$ , abbreviated $\displaystyle \sin \theta$ , is the ratio between the opposite side and the hypotenuse of a triangle. For instance, in the 30-60-90 triangle above, $\sin 30=\frac 12$ .

Cosine

The cosine of an angle $\theta$ , abbreviated $\displaystyle \cos \theta$ , is the ratio between the adjacent side and the hypotenuse of a triangle. For instance, in the 30-60-90 triangle above, $\cos 30=\frac{\sqrt{3}}{2}$ .

Tangent

The tangent of an angle $\theta$ , abbreviated $\displaystyle \tan \theta$ , is the ratio between the opposite side and the adjacent side of a triangle. For instance, in the 30-60-90 triangle above, $\tan 30=\frac{\sqrt{3}}{3}$ . (Note that $\tan \theta=\frac{\sin\theta}{\cos\theta}$ .)

Cosecant

The cosecant of an angle $\theta$ , abbreviated $\displaystyle \csc \theta$ , is the ratio between the hypotenuse and the opposite side of a triangle. For instance, in the 30-60-90 triangle above, $\displaystyle \csc 30=2$ . (Note that $\csc \theta=\frac{1}{\sin \theta}$ .)

Secant

The secant of an angle $\theta$ , abbreviated $\displaystyle \sec \theta$ , is the ratio between the hypotenuse and the adjacent side of a triangle. For instance, in the 30-60-90 triangle above, $\sec 30=\frac{2\sqrt{3}}{3}$ . (Note that $\sec \theta=\frac{1}{\cos \theta}$ .)

Cotangent

The cotangent of an angle $\theta$ , abbreviated $\displaystyle \cot \theta$ , is the ratio between the adjacent side and the opposite side of a triangle. For instance, in the 30-60-90 triangle above, $\cot 30=\sqrt{3}$ . (Note that $\cot \theta=\frac{\cos\theta}{\sin\theta}$ .)

Page

Toolbox

Search