1991 AIME Problems/Problem 11

Problem

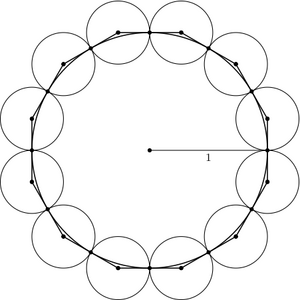
Twelve congruent disks are placed on a circle $C^{}_{}$ of radius 1 in such a way that the twelve disks cover $C^{}_{}$ , no two of the disks overlap, and so that each of the twelve disks is tangent to its two neighbors. The resulting arrangement of disks is shown in the figure below. The sum of the areas of the twelve disks can be written in the from $\pi(a-b\sqrt{c})$ , where $a,b,c^{}_{}$ are positive integers and $c^{}_{}$ is not divisible by the square of any prime. Find $a+b+c^{}_{}$ .

Solution

We wish to find the radius of one circle, so that we can find the total area.

Notice that for them to contain the entire circle, each pair of circles must be tangent on the larger circle. Now consider two adjacent smaller circles. This means that the line connecting the radii is a segment of length $2r$ that is tangent to the larger circle at the midpoint of the two centers. Thus, we have essentially have a regular dodecagon whose vertices are the centers of the smaller triangles circumscribed about a circle of radius $1$ .

We thus know that the apothem of the dodecagon is equal to $1$ . To find the side length, we make a triangle consisting of a vertex, the midpoint of a side, and the center of the dodecagon, which we denote $A, M,$ and $O$ respectively. Notice that $OM=1$ , and that $\triangle OMA$ is a right triangle with hypotenuse $OA$ and $m \angle MOA = 15^\circ$ . Thus $AM = (1) \tan{15^\circ} = 2 - \sqrt {3}$ , which is the radius of one of the circles. The area of one circle is thus $\pi(2 - \sqrt {3})^{2} = \pi (7 - 4 \sqrt {3})$ , so the area of all $12$ circles is $\pi (84 - 48 \sqrt {3})$ , giving an answer of $84 + 48 + 3 = \boxed{135}$ .

1991 AIME (Problems • Answer Key • Resources)
Preceded by Problem 10	Followed by Problem 12
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search

1991 AIME Problems/Problem 11

Problem

Solution

See also