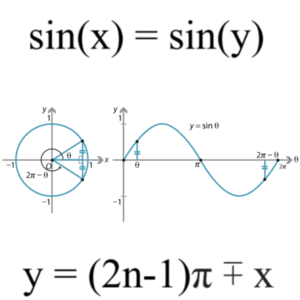Jadhav Sin Function Theorem

Jadhav's Sine Function Theorem helps in finding value of infinite angles which form same sine function ratio with know one angle. This Formula based theorem is a superior alternative to complex sine function theorem. It is an pure result of patterns seen in the angular measure of the sin inverse ratios.

This theorem is all based on old nomenclature and notations which states.

If $sin(x)=sin(y)$ such that $x,y \in R$

then $y = (2n-1)\pi^c + x$ or $y = (2n-1)180^\circ - x$

Constants

There is only one constant in the theorem $\pi^c$ / $180^\circ$ . $\pi^c$ is used if the angle $x$ is in radian measure and $180^\circ$ is used if angle $x$ is in degree measure.

Units

Angle $y$ is obtained in the respective angular measures on the use of constants, if $\pi^c$ is used then the resultant angle $y$ is obtained in radians, if $180^\circ$ is used then resultant angle would be in degrees.

Explanation

You need to know one angle for which sine function makes a angle and now to find other angles for which it forms same ratio then we can use the rules given below and find infinitely many angles:

To get y as positive i.e. other positive angles for which sine ratio remains same, n should always equal to 1 or above $y = (2n-1)\pi^c + x$
To get y as negative i.e. Negative angle for which sine ratio remains same, n should always equal to 0 or values below it. $y = (2n-1)180^\circ - x$
This theorem even works if x is a negative angle and would follow the same two rules given above with any sign of angle.

This article has been proposed for deletion. The reason given is: lacks notability Sysops: Before deleting this article, please check the article discussion pages and history.

Page

Toolbox

Search

Jadhav Sin Function Theorem

Constants

Units

Explanation