2024 AMC 12A Problems/Problem 13

Problem

The graph of $y=e^{x+1}+e^{-x}-2$ has an axis of symmetry. What is the reflection of the point $(-1,\tfrac{1}{2})$ over this axis?

$\textbf{(A) }\left(-1,-\frac{3}{2}\right)\qquad\textbf{(B) }(-1,0)\qquad\textbf{(C) }\left(-1,\frac{1}{2}\right)\qquad\textbf{(D) }\left(0,\frac{1}{2}\right)\qquad\textbf{(E) }\left(3,\frac{1}{2}\right)$

Solution 1

The line of symmetry is probably of the form $x=a$ for some constant $a$ . A vertical line of symmetry at $x=a$ for a function $f$ exists if and only if $f(a-b)=f(a+b)$ ; we substitute $a-b$ and $a+b$ into our given function and see that we must have

$e^{a-b+1}+e^{-(a-b)}-2=e^{a+b+1}+e^{-(a+b)}-2$

for all real $b$ . Simplifying:

\begin{align*} e^{a-b+1}+e^{-(a-b)}-2&=e^{a+b+1}+e^{-(a+b)}-2 \\ e^{a-b+1}+e^{b-a}&=e^{a+b+1}+e^{-a-b} \\ e^{a-b+1}-e^{-a-b}&=e^{a+b+1}-e^{b-a} \\ e^{-b}\left(e^{a+1}-e^{-a}\right)&=e^b\left(e^{a+1}-e^{-a}\right). \\ \end{align*}

If $e^{a+1}-e^{-a}\neq0$ , then $e^{-b}=e^b$ for all real $b$ ; this is clearly impossible, so let $e^{a+1}-e^{-a}=0\implies a+1=-a\implies a=-\dfrac12$ . Thus, our line of symmetry is $x=-\dfrac12$ , and reflecting $\left(-1,\dfrac12\right)$ over this line gives $\boxed{\textbf{(D) }\left(0,\dfrac12\right)}.$

~Technodoggo

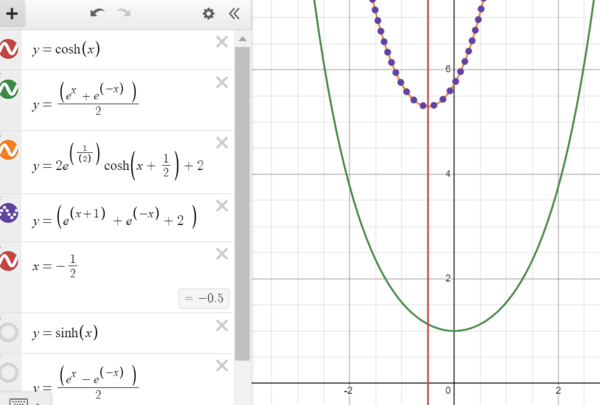
Solution 2 (Graphing cheese)

Consider the graphs of $y=e^{x+1}-1$ and $y=e^{-x}-1$ . A rough sketch will show that they intercept somewhere between -1 and 0 and the axis of symmetry is vertical. Thus, $\boxed{\textbf{(D) }\left(0,\dfrac12\right)}$ is the only possible answer.

Note: You can more rigorously think about the solution by noting that since the derivative of the power that e is raised to in one equation is equal to the derivative of the power that e is raised to multiplied by $-1$ and both equations are subtracted by 1, then the sum of both equations will be the same from one side of the interception to the other. Setting both equations equal to each other, it is trivial to see $x=-1/2$ , giving us the axis of symmetry.

~woeIsMe

$[asy] unitsize(2cm); real e = 2.71828; real f1(real x) {return e^(x+1)-1;} real f2(real x) {return e^(0-x)-1;} draw(graph(f1,-1.5,0.5)); draw(graph(f2,-1.5,0.5)); xaxis(-2,1,Ticks()); yaxis(f2(0.5),f1(0.5),Ticks()); draw((-0.5,f2(0.5))--(-0.5,f1(0.5)),red+dashed); /*graph by Technodoggo, 9 November 2024*/ [/asy]$ (graph by Technodoggo)

Solution 3 (Derivatives)

Since y is a proper function of x, the axis of symmetry is vertical (and so answer choices A and B are impossible). Where a function crosses a vertical axis of symmetry, it must have either a vertical asymptote (clearly impossible for this given function, since linear functions and exponential function are total functions) or a local maximum or minimum (derivative 0).

So the derivative is equal to 0: $\frac{d[e^{x+1}+e^{-x}-2]}{dx} = 0 = e^{x+1}-e^{-x}$

To solve for $x$ , make a substitution: $u = e^x$ $0 = e*u - \frac{1}{u}$ -> $0 = \frac{e*u^2 - 1}{u}$ -> $0 = e*u^2 - 1$ -> $e*u^2 = 1$ -> $(e^x)^2 = \frac{1}{e}$ -> $e^{2x} = e^{-1}$ -> $2x = -1$ -> $x = -\frac{1}{2}$

Reflect $\left(-1, \frac{1}{2}\right)$ over $x = -\frac{1}{2}$ , giving answer choice $\boxed{\textbf{(D) }\left(0,\dfrac12\right)}.$

Solution 4

$f(0) = e-1$ $f(1) = e^2 + e^{-1} - 2$ $f(-1) = 1+ e -2 = e-1$ $f(-2) = e^{-1} + e^2 -2$

so f(0) = f(-1) , f(1) =f(-2) then f(x) is symmetric about x=-1/2 point (-1, 1/2) reflects over axis x=-1/2 is point ( 0, 1/2) answer choice D ~luckuso

Solution 5

Notice that this is simply a transformation of $\cosh(x)$ , specifically $2e^\frac{1}{2}\cosh(x + \frac{1}{2}) + 2$ . We know that $\cosh(x)$ has a parabolic shape with an axis of symmetry $x=0$ . Since this is simple a transformation of $\frac{1}{2}$ to the left of the origin, we have the axis of symmetry is $x = -\frac{1}{2}$ giving us $\boxed{\textbf{(D) }\left(0,\dfrac12\right)}$

~KEVIN_LIU

Solution 5 (Graph)

~luckuso

Solution 6

$f(-x-1) = e^{-x-1+1} + e^{-(-x-1)} - 2 = e^{-x} + e^{x+1} - 2 = f(x)$

So the axis is $\frac{x + (-x + 1)}{2} = -1/2$

Point $(-1, 1/2)$ reflects over the axis $x=-1/2$ to the point $\boxed{\textbf{(D) }\left(0,\dfrac12\right)}$

~luckuso

Solution 7

Setting the axis of symmetry as $x=a$ implies $f(2a-x) = f(x)$

$\begin{align*} f(2a-x) &= f(x) \\ e^{2a-x+1} + e^{-(2a-x)} - 2 &= e^{x+1} + e^{-x} - 2 \end{align*}$

Analyzing the terms $e^{2a-x+1}$ and $e^{-x}$ tells us that $2a+1 = 0$

This reveals that $a = -1/2$

Finally, point $(-1, 1/2)$ reflected over the axis $x=-1/2$ is the point $\boxed{\textbf{(D) }\left(0,\dfrac12\right)}$

~luckuso

2024 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 12	Followed by Problem 14
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search

2024 AMC 12A Problems/Problem 13

Contents

Problem

Solution 1

Solution 2 (Graphing cheese)

Solution 3 (Derivatives)

Solution 4

Solution 5

Solution 5 (Graph)

Solution 6

Solution 7

See also