2024 AMC 12B Problems/Problem 12
Problem
Let ![]() be a complex number with real part greater than
be a complex number with real part greater than ![]() and
and ![]() . In the complex plane, the four points
. In the complex plane, the four points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are the vertices of a quadrilateral with area
are the vertices of a quadrilateral with area ![]() . What is the imaginary part of
. What is the imaginary part of ![]() ?
?
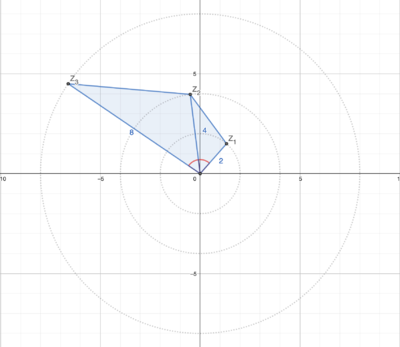
Diagram
Solution 1 (similar triangles)
By making a rough estimate of where ![]() ,
, ![]() , and
, and ![]() are on the complex plane, we can draw a pretty accurate diagram (like above.)
are on the complex plane, we can draw a pretty accurate diagram (like above.)
Here, points ![]() ,
, ![]() , and
, and ![]() lie at the coordinates of
lie at the coordinates of ![]() ,
, ![]() , and
, and ![]() respectively, and
respectively, and ![]() is the origin.
is the origin.
We're given ![]() , so
, so ![]() and
and ![]() . This gives us
. This gives us ![]() ,
, ![]() , and
, and ![]() .
.
Additionally, we know that ![]() (since every power of
(since every power of ![]() rotates around the origin by the same angle.) We set these angles equal to
rotates around the origin by the same angle.) We set these angles equal to ![]() .
.
This gives us enough info to say that ![]() by SAS (since
by SAS (since ![]() .)
.)
It follows that ![]() as the ratio of side lengths of the two triangles is 2 to 1.
as the ratio of side lengths of the two triangles is 2 to 1.
This means ![]() or
or ![]() as we were given
as we were given ![]() .
.
Using ![]() , we get that
, we get that ![]() , so
, so ![]() , giving
, giving ![]() .
.
Thus, ![]() .
.
~nm1728