Discriminant
The discriminant of a quadratic equation of the form ![]() is the quantity
is the quantity ![]() . When
. When ![]() are real, this is a notable quantity, because if the discriminant is positive, the equation has two real roots; if the discriminant is negative, the equation has two nonreal roots; and if the discriminant is 0, the equation has a real double root.
are real, this is a notable quantity, because if the discriminant is positive, the equation has two real roots; if the discriminant is negative, the equation has two nonreal roots; and if the discriminant is 0, the equation has a real double root.
Contents
Discriminant of polynomials of degree n
The discriminant can tell us something about the roots of a given polynomial ![]() of degree
of degree ![]() with all the coefficients being real. But for polynomials of degree 4 or higher it can be difficult to use it.
with all the coefficients being real. But for polynomials of degree 4 or higher it can be difficult to use it.
General formula of discriminant
We know that the discriminant of a polynomial is the product of the squares of the differences of the polynomial roots ![]() , so,
, so,

When 
Given a polynomial ![]() , its discriminant is
, its discriminant is ![]() , which can also be denoted by
, which can also be denoted by ![]() .
.
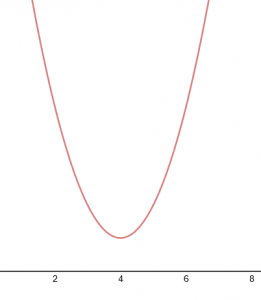
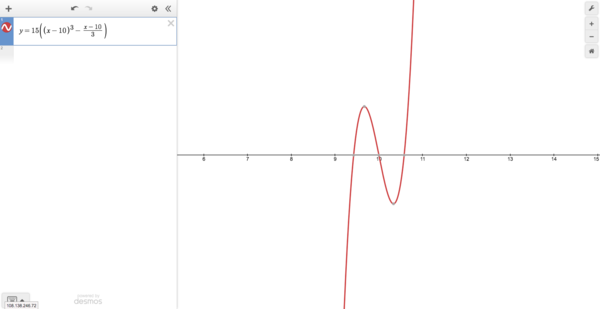
For ![]() we have the graph
we have the graph
which has two distinct real roots.
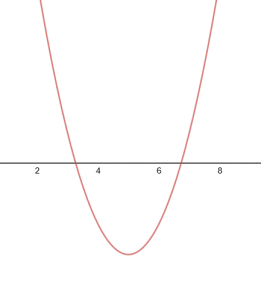
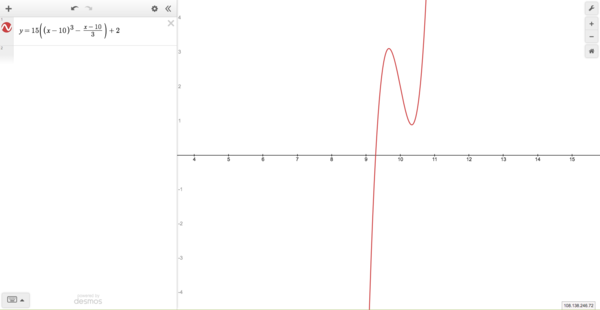
For ![]() we have the graph
we have the graph
which has two non-real roots.
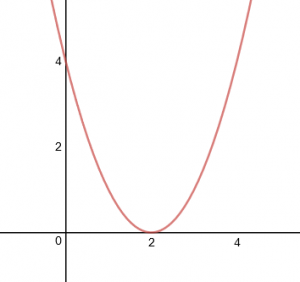
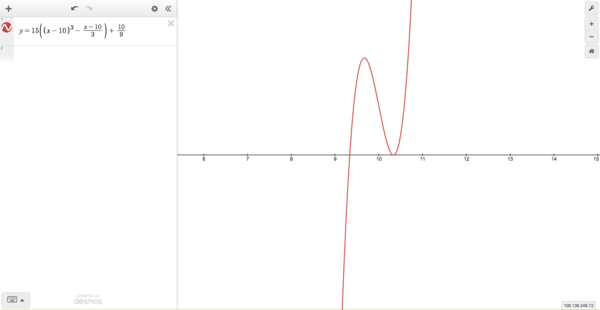
And for the case ![]() ,
,
When 
The discriminant of a polynomial ![]() is given by
is given by ![]() .
.
Also, the depressed cubic form ![]() has discriminant
has discriminant ![]() . We can compress a polynomial of degree 3, which also makes possible to us to use Cardano's formula, by doing the substitution
. We can compress a polynomial of degree 3, which also makes possible to us to use Cardano's formula, by doing the substitution ![]() on the polynomial
on the polynomial ![]() .
.
- If
 , then at least two of the roots are equal;
, then at least two of the roots are equal;
- If
 , then all three roots are real and distinct;
, then all three roots are real and distinct;
- If
 , then one of the roots is real and the other two are complex conjugate.
, then one of the roots is real and the other two are complex conjugate.
When 
The quartic polynomial ![]() has discriminant
has discriminant
![]()
- If
 , then at least two of the roots are equal;
, then at least two of the roots are equal; - If
 , then the roots are all real or all non-real;
, then the roots are all real or all non-real; - If
 , then there are two real roots and two complex conjugate roots.
, then there are two real roots and two complex conjugate roots.
Some properties
For ![]() we can say that
we can say that
- The polynomial has a multiple root if, and only if,
 ;
; - If
 , with
, with  being a positive integer such that
being a positive integer such that  , with
, with  being the degree of the polynomial, then there are
being the degree of the polynomial, then there are  pairs of complex conjugate roots and
pairs of complex conjugate roots and  real roots;
real roots; - If
 , with
, with  being a positive integer such that
being a positive integer such that  , then there are
, then there are  pairs of complex conjugate roots and
pairs of complex conjugate roots and  real roots.
real roots.
Example Problems
Introductory
- (AMC 12 2005) There are two values of
 for which the equation
for which the equation  has only one solution for
has only one solution for  . What is the sum of these values of
. What is the sum of these values of  ?
?
Solution: Since we want the ![]() 's where there is only one solution for
's where there is only one solution for ![]() , the discriminant has to be
, the discriminant has to be ![]() .
. ![]() . The sum of these values of
. The sum of these values of ![]() is
is ![]() .
.