DVI exam
2022 221 problem 7
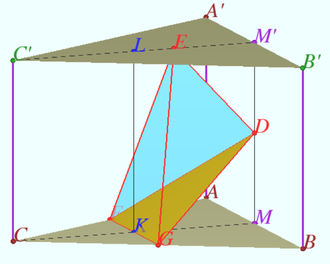
The volume of a triangular prism 
with base 
and side edges 
is equal to 
Find the volume of the tetrahedron 
where 
is the centroid of the face 
is the point of intersection of the medians of 
is the midpoint of the edge 
and 
is the midpoint of the edge 
Solution
Let us consider the uniform triangular prism 
Let 
be the midpoint of 
be the midpoint of 
be the midpoint of 
be the midpoint of 
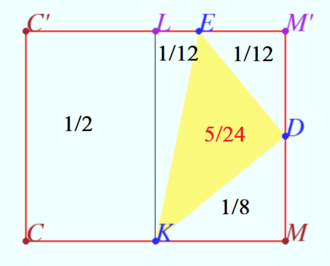
The area ![$[KED]$](http://latex.artofproblemsolving.com/f/b/a/fba57621447876aa5fd27d1e0dcafd32131a1bbd.png)
of 
in the sum with the areas of triangles ![$[KEL], [EDM'], [KDM]$](http://latex.artofproblemsolving.com/f/1/9/f19629b2cd5a7d03bc75888eb448b289d2031c3b.png)
is half the area of rectangle 
so
![\[\frac {[KED]}{[CC'M'M]} = \frac {1}{2} - \frac {1}{12}- \frac {1}{12}-\frac {1}{8} = \frac {5}{24}.\]](http://latex.artofproblemsolving.com/8/2/2/82288c2b393f8c31ad458f17922c8d8b09613d18.png)
![\[FG \perp ED.\]](http://latex.artofproblemsolving.com/1/d/0/1d04737c3f8ff9ca13b3b77a0d1953b3fe707c35.png)
Denote the distance between these lines 
The volume of the tetrahedron is 
![\[\frac {ED \cdot h}{2} = \frac {5}{24} \cdot CC' \cdot CM \implies U =\frac{5}{24 \cdot 3} \cdot CC' \cdot CM \cdot FG.\]](http://latex.artofproblemsolving.com/4/7/8/4788957d32d443cee46dc23c549a2567a6f5bd88.png)
The volume of the prism is 
![\[\frac {U}{V} = \frac {\frac {5}{72} CC' \cdot CM \cdot FG}{CC' \cdot CM \cdot FG} = \frac {5}{72} \implies U = 5.\]](http://latex.artofproblemsolving.com/b/c/1/bc112e33f6cf11d8285c38145ecd3a0f9b2b4faa.png)
An arbitrary prism is obtained from a regular one as a result of an affine transformation.
All points on the tetrahedron are defined affinely, which means that the volume ratio will be preserved.
Answer: 5.
2022 222 problem 7
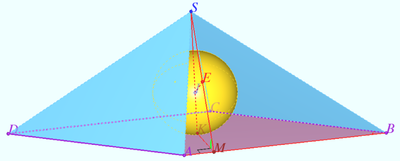
A sphere of diameter 
is inscribed in a pyramid at the base of which lies a rhombus with an acute angle 
and side 
Find the angle if it is known that all lateral faces of the pyramid are inclined to plane of its base at an angle of 
Solution 1
Denote rhombus 
is the vertex of a pyramid 
is the center of the sphere, 
is the tangent point of 
and sphere, 
![\[IE = r, SK = SI + IK = \frac {3}{2}, KM = \frac {\sqrt{3}}{2}, SM = \sqrt{3}.\]](http://latex.artofproblemsolving.com/1/e/b/1ebd793d2268ad58c514225131e833858d042f23.png)
![\[AM = KM \cdot \tan \alpha, BM = \frac {KM}{\tan \alpha},\]](http://latex.artofproblemsolving.com/2/b/c/2bc88738c2efa898feb0c22b93dc8754aa27f8d8.png)
![\[AM + BM = AB = \sqrt{6}\implies\]](http://latex.artofproblemsolving.com/3/b/7/3b79cd17e4b558e64a8b1f514007ebe95da24557.png)
![\[\tan \alpha + \frac {1}{\tan \alpha} = 2 \sqrt {2} \implies \tan \alpha = \sqrt {2} - 1 \implies \tan 2 \alpha = 1 \implies 2 \alpha = \frac {\pi}{4}.\]](http://latex.artofproblemsolving.com/a/d/9/ad94bbf8346d00722305ab7c3dca276520748cb6.png)
Solution 2
The area of the rhombus ![$[ABCD]= AB^2 \cdot \sin 2\alpha.$](http://latex.artofproblemsolving.com/7/1/9/71943de9a1d67756d77ec273ff85ee2cd1044898.png)
The area of the lateral surface is ![$[l]= 4 [SAB] = 2 \cdot AB \cdot SM.$](http://latex.artofproblemsolving.com/b/5/7/b57349997a507aab95d3f3c03357ea2065754ecb.png)
![\[[ABCD] = [l] \cdot \cos 60 ^\circ =[l] \cdot \frac{1}{2} \implies AB \cdot SM = AB^2 \cdot \sin 2\alpha \implies\]](http://latex.artofproblemsolving.com/5/6/9/5690be5735e2b7558af617c1fadf380ba8a1084e.png)
![\[\sin {2 \alpha} = \frac {SM}{AB} = \frac {\sqrt{3}}{\sqrt{6}} = \frac {1}{\sqrt{2}}.\]](http://latex.artofproblemsolving.com/5/7/9/57999904bddd7720f46679becac301321c7f3911.png)
Answer:
