1991 OIM Problems/Problem 2

Problem

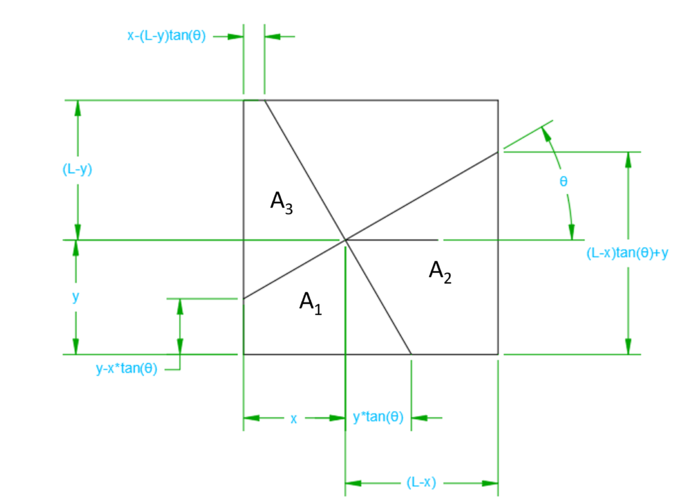
Two perpendicular lines divide a square into four parts, three of which each have an area equal to 1. Show that the area of the square is four.

~translated into English by Tomas Diaz. ~orders@tomasdiaz.com

Solution

First let's find the area of $A_1$ :

$A_1=x\frac{y-x.tan(\theta)+y}{2}+\frac{y^2tan(\theta)}{2}$

$A_1=\frac{y^2-x^2}{2}tan(\theta)+xy=1$

Now lets find the area of $A_2$ :

$A_2=\frac{L-x}{2}((L-x)tan(\theta)+y+y)-\frac{y^2}{2}tan(\theta)$

$A_2=\frac{(L-x)^2-y^2}{2}tan(\theta)+(L-x)y=1$

Now lets find the area of $A_3$ :

$A_3=\frac{L-y}{2}(x+x-(L-y)tan(\theta))+\frac{x^2}{2}tan(\theta)$

$A_3=\frac{x^2-(L-y)^2}{2}tan(\theta)+x(L-y)=1$

Now we need to solve for $x$ , $y$ and $L$ in the following system of equations:

$\begin{cases} \frac{y^2-x^2}{2}tan(\theta)+xy=1\\ \frac{(L-x)^2-y^2}{2}tan(\theta)+(L-x)y=1\\ \frac{x^2-(L-y)^2}{2}tan(\theta)+x(L-y)=1 \end{cases}$

We need the solution to be independent of $tan(\theta)$ , so the coefficient in front of that in all three equations need to be zero. Starting with the first equation we can find that condition and see if the conditions holds in the other two equations. Therefore,

$\frac{y^2-x^2}{2}=0$ which means that $x=y$

Thus,

$\frac{y^2-x^2}{2}tan(\theta)+xy=xy=1$ and since $x=y$ , then $x=y=1$

We substitute in the next two equations:

$\begin{cases} \frac{(L-1)^2-1^2}{2}tan(\theta)+(L-1)=1\\ \frac{1^2-(L-1)^2}{2}tan(\theta)+(L-1)=1 \end{cases}$

Note. I actually competed at this event in Argentina when I was in High School representing Puerto Rico. I got partial points because I couldn't prove this but had somewhat of an approach to get there.

~Tomas Diaz. orders@tomasdiaz.com

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

Page

Toolbox

Search

1991 OIM Problems/Problem 2

Problem

Solution

See also