Mock AIME 2 2006-2007 Problems/Problem 15
Contents
Problem
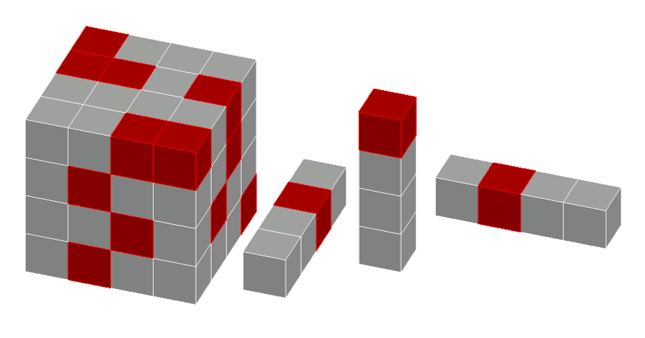
A ![]() cube is composed of
cube is composed of ![]() unit cubes. The faces of
unit cubes. The faces of ![]() unit cubes are colored red. An arrangement of the cubes is "intriguing" if there is exactly
unit cubes are colored red. An arrangement of the cubes is "intriguing" if there is exactly ![]() red unit cube in every
red unit cube in every ![]() rectangular box composed of
rectangular box composed of ![]() unit cubes. Determine the number of "intriguing" colorings.
unit cubes. Determine the number of "intriguing" colorings.
Solution
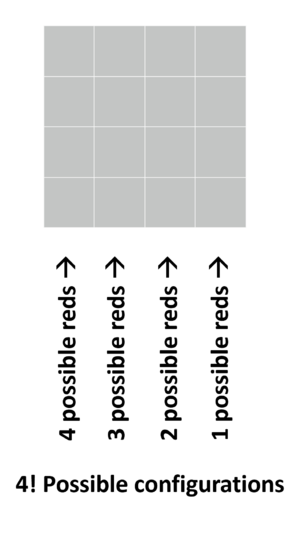
In order to solve this we must first look at the 2D problem:
In order to have exactly one red in each column and exactly one red in each row of the 4x4 grid, one can select any square red in the first column, for the second column we can only chose from 3 to paint red, the third column we can only chose 2 and the last one we can only chose 1.
Therefore the total numbers of squares that can have exactly one red in each column and exactly one red in each row and one red in each row is exactly ![]()
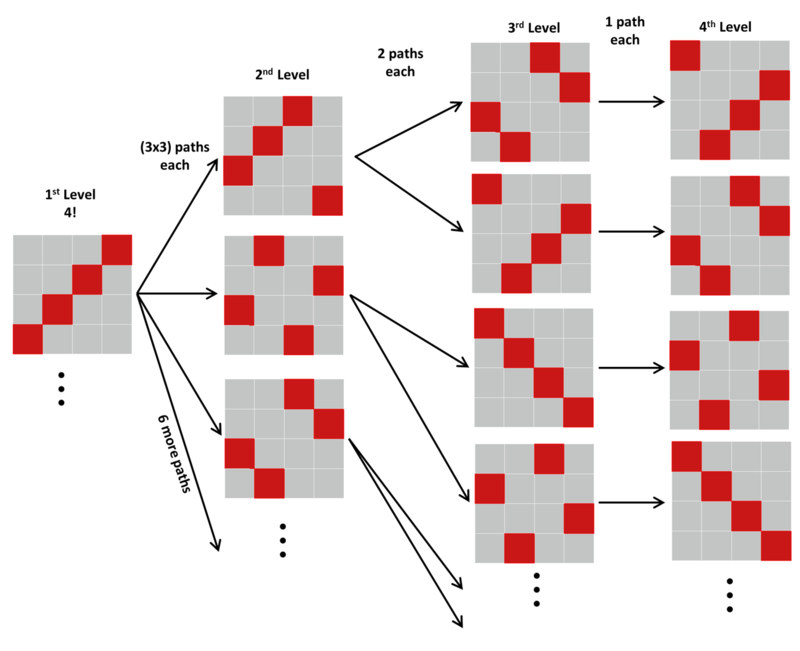
Now we can use this information for the 3D problem by looking at each of these squares as levels of the cube starting with the first level that has 4! configurations.
Starting with the first level configuration as shown above, this configuration has three possible paths to the next level square grid to squares where the red square of the first column is the the one in the 3rd row as shown. Not shown in the image this configuration will have three more possible paths to squares where the red square of the first column is the the one in the 2nd row, and three red square of the first column is the the one in the 2nd row. That is a total of 9 paths.
Then each of these configurations on the 2nd level will have 2 paths each to the 3rd level as shown. Only one path is left from the 3rd level to the 4th level for each of the configurations.
Therefore the total number of "intriguing" colorings will be the product of all paths:
![]() "intriguing" colorings.
"intriguing" colorings.
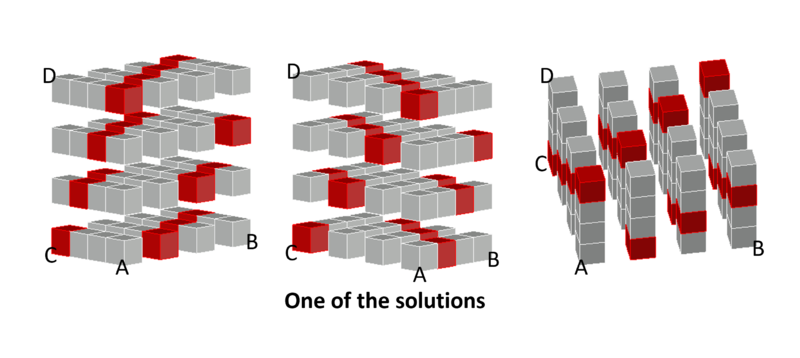
Here is an example of one of such "intriguing" colorings:
See Also
| Mock AIME 2 2006-2007 (Problems, Source) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||