Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2007 IMO Shortlist Problems/G3

Revision as of 12:33, 2 March 2023 by Vvsss (talk | contribs) (→‎IMO 2007 Short list)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)

IMO 2007 Short list/G3

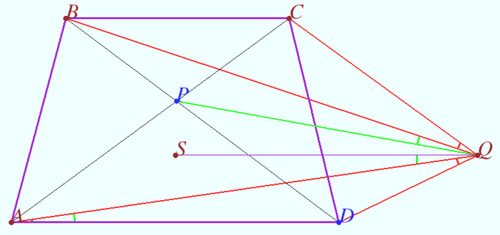
Trapezoid 17.png

The diagonals of a trapezoid $ABCD$ intersect at point $P.$

Point $Q$ lies between the parallel lines $BC$ and $AD$ such that $\angle AQD = \angle CQB,$ and line $CD$ separates points $P$ and $Q.$

Prove that $\angle BQP = \angle DAQ.$

Proof

$\angle AQD = \angle CQB \implies$

$BQ$ and $AQ$ are isogonals with respect $\angle CQD.$

$P =AC \cap BD, BC || AD \implies$

$QS || AD$ is isogonal to $QP$ with respect $\angle CQD.$

From the converse of The isogonal theorem we get

$\angle BQP = \angle SQA = \angle DAQ.$ $\blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2007_IMO_Shortlist_Problems/G3&oldid=190506"