2023 AMC 8 Problems/Problem 12

Problem

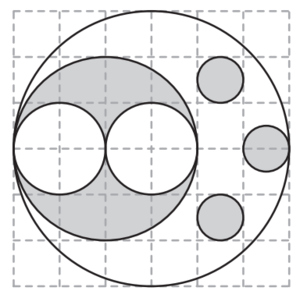
The figure below shows a large white circle with a number of smaller white and shaded circles in its interior. What fraction of the interior of the large white circle is shaded?

$\textbf{(A)}\ \frac{1}{4} \qquad \textbf{(B)}\ \frac{11}{36} \qquad \textbf{(C)}\ \frac{1}{3} \qquad \textbf{(D)}\ \frac{19}{36} \qquad \textbf{(E)}\ \frac{5}{9}$

Solution 1

First the total area of the $3$ radius circle is simply just $9* \pi$ . Using our area of a circle formula.

Now from here we have to find our shaded area. This can be done by adding the areas of the $3$ $\frac{1}{2}$ radius circles and add then take the area of the $2$ radius circle and subtracting that from the area of the $2$ , 1 radius circles to get our resulting complex area shape. Adding these up we will get $3 * \frac{1}{4} \pi + 4 \pi -\pi - \pi = \frac{3}{4} \pi + 2 \pi = \frac{11}{4}$

Our answer is $\frac {\frac{11}{4} \pi}{9 \pi} = \boxed{\textbf{(B)}\ \frac{11}{36}}$

~apex304

Solution 2

Pretend each circle is a square. The second largest circle is a square with area $16 \text{units}^2$ and there are two squares in that square that each have area $4\text{units}^2$ which add up to 8. Subtracting the medium-sized squares' areas from the second-largest square's area, we have $8\text{units}^2$ . The largest circle becomes a square that has area $36\text{units}^2$ , and the three smallest circles become three squares with area $8\text{units}^2$ and add up to $3^2$ . Adding the areas of the shaded regions we get $11$ , so our answer is $\boxed{\textbf{(B)}\ \dfrac{11}{36}}$ .