2022 AMC 8 Problems/Problem 25

Problem

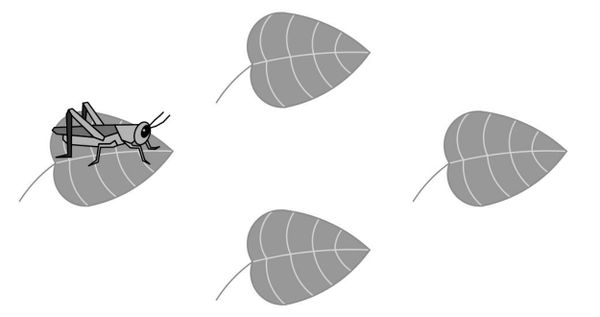
A cricket randomly hops between $4$ leaves, on each turn hopping to one of the other $3$ leaves with equal probability. After $4$ hops what is the probability that the cricket has returned to the leaf where it started?

$\textbf{(A) }\frac{2}{9}\qquad\textbf{(B) }\frac{19}{80}\qquad\textbf{(C) }\frac{20}{81}\qquad\textbf{(D) }\frac{1}{4}\qquad\textbf{(E) }\frac{7}{27}$

Solution 1 (Casework)

Let $A$ denote the leaf where the cricket starts and $B$ denote one of the other $3$ leaves. Note that:

If the cricket is at $A,$ then the probability that it hops to $B$ next is $1.$

If the cricket is at $B,$ then the probability that it hops to $A$ next is $\frac13.$

If the cricket is at $B,$ then the probability that it hops to $B$ next is $\frac23.$

We apply casework to the possible paths of the cricket:

$A \rightarrow B \rightarrow A \rightarrow B \rightarrow A$
The probability for this case is $1\cdot\frac13\cdot1\cdot\frac13=\frac19.$

$A \rightarrow B \rightarrow B \rightarrow B \rightarrow A$
The probability for this case is $1\cdot\frac23\cdot\frac23\cdot\frac13=\frac{4}{27}.$

Together, the probability that the cricket returns to $A$ after $4$ hops is $\frac19+\frac{4}{27}=\boxed{\textbf{(E) }\frac{7}{27}}.$

~MRENTHUSIASM

Solution 2 (Casework)

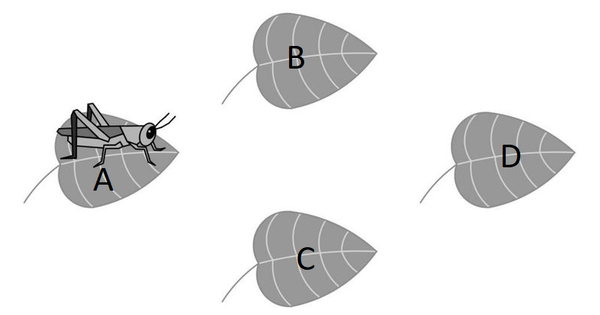
We can label the leaves as shown below:

Carefully counting cases, we see that there are $7$ ways for the cricket to return to leaf $A$ after four hops if its first hop was to leaf $B$ :

$A \rightarrow B \rightarrow A \rightarrow B \rightarrow A$

$A \rightarrow B \rightarrow A \rightarrow C \rightarrow A$

$A \rightarrow B \rightarrow A \rightarrow D \rightarrow A$

$A \rightarrow B \rightarrow C \rightarrow B \rightarrow A$

$A \rightarrow B \rightarrow C \rightarrow D \rightarrow A$

$A \rightarrow B \rightarrow D \rightarrow B \rightarrow A$

$A \rightarrow B \rightarrow D \rightarrow C \rightarrow A$

By symmetry, we know that there are $7$ ways if the cricket's first hop was to leaf $C$ , and there are $7$ ways if the cricket's first hop was to leaf $D$ . So, there are $21$ ways in total for the cricket to return to leaf $A$ after four hops.

Since there are $3^4 = 81$ possible ways altogether for the cricket to hop to any other leaf four times, the answer is $\frac{21}{81} = \boxed{\textbf{(E) }\frac{7}{27}}$ .

~mahaler

Solution 3 (Recursion)

Denote $P_n$ to be the probability that the cricket would return back to the first point after $n$ hops. Then, we get the recursive formula $P_n = \frac13(1-P_{n-1})$ because if the leaf is not on the target leaf, then there is a $\frac13$ probability that it will make it back.

With this formula and the fact that $P_1=0$ (After one hop, the cricket can never be back to the target leaf.), we have $P_2 = \frac13, P_3 = \frac29, P_4 = \frac7{27},$ so our answer is $\boxed{\textbf{(E) }\frac{7}{27}}$ .

~wamofan

Solution 4 (Dynamic Programming)

Let $A$ denote the leaf cricket starts at, and $B, C, D$ be the other leaves, similar to Solution 2.

Let $A(n)$ be the probability the cricket lands on $A$ after $n$ hops, $B(n)$ be the probability the cricket lands on $B$ after crawling $n$ hops, and etc.

Note that $A(1)=0$ and $B(1)=C(1)=D(1)=\frac13.$ For $n\geq2,$ the probability that the cricket land on each leaf after $n$ hops is $\frac13$ the sum of the probability the cricket land on other leaves after $n-1$ hops. So, we have $\begin{align*} A(n) &= \frac13 \cdot [B(n-1) + C(n-1) + D(n-1)], \\ B(n) &= \frac13 \cdot [A(n-1) + C(n-1) + D(n-1)], \\ C(n) &= \frac13 \cdot [A(n-1) + B(n-1) + D(n-1)], \\ D(n) &= \frac13 \cdot [A(n-1) + B(n-1) + C(n-1)]. \end{align*}$ It follows that $A(n) = B(n-1) = C(n-1) = D(n-1).$

We construct the following table: $\begin{array}{c|cccc} & & & & \\ [-2ex] n & A(n) & B(n) & C(n) & D(n) \\ [1ex] \hline & & & & \\ [-1ex] 1 & 0 & \frac13 & \frac13 & \frac13 \\ & & & & \\ 2 & \frac13 & \frac29 & \frac29 & \frac29 \\ & & & & \\ 3 & \frac29 & \frac{7}{27} & \frac{7}{27} & \frac{7}{27} \\ & & & & \\ 4 & \frac{7}{27} & \frac{20}{81} & \frac{20}{81} & \frac{20}{81} \\ [1ex] \end{array}$ Therefore, the answer is $A(4)=\boxed{\textbf{(E) }\frac{7}{27}}$ .

~isabelchen

Solution 5 (Generating Function)

Assign the leaves to $0, 1, 2,$ and $3$ modulo $4,$ and let $0$ be the starting leaf. We then use generating functions with relation to the change of leaves. For example, from $3$ to $1$ would be a change of $2,$ and from $1$ to $2$ would be a change of $1.$ This generating function is equal to $(x+x^2+x^3)^4.$ It is clear that we want the coefficients in the form of $x^{4n},$ where $n$ is a positive integer. One application of roots of unity filter gives us a successful case count of $\frac{81+1+1+1}{4} = 21.$

Therefore, the answer is $\frac{21}{3^4}=\boxed{\textbf{(E) }\frac{7}{27}}.$

~sigma

Remark

This problem is a reduced version of 1985 AIME Problem 12, changing $7$ steps into $4$ steps.

This problem is also similar to 2003 AIME II Problem 13.

~isabelchen

Video Solution

https://youtu.be/GNFG4cmYDgw

Please like and subscribe!

Video Solution

https://www.youtube.com/watch?v=85A6av3oqRo

~Mathematical Dexterity

Video Solution

https://youtu.be/Ij9pAy6tQSg?t=2588

~Interstigation

Video Solution

https://www.youtube.com/watch?v=H1zxrkq6DKg

Video Solution

https://youtu.be/0orAAUaLIO0?t=609

~STEMbreezy

Video Solution

https://youtu.be/9SKUdTut3l4

~savannahsolver

2022 AMC 8 (Problems • Answer Key • Resources)
Preceded by Problem 24	Followed by Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AJHSME/AMC 8 Problems and Solutions

Page

Toolbox

Search

2022 AMC 8 Problems/Problem 25

Contents

Problem

Solution 1 (Casework)

Solution 2 (Casework)

Solution 3 (Recursion)

Solution 4 (Dynamic Programming)

Solution 5 (Generating Function)

Remark

Video Solution

Video Solution

Video Solution

Video Solution

Video Solution

Video Solution

See Also