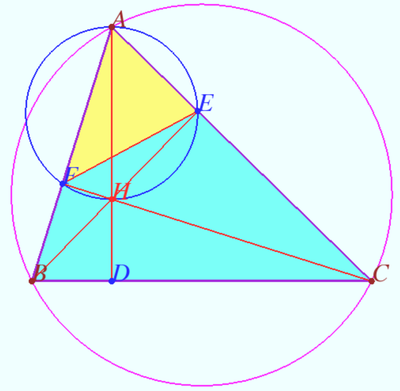
Kimberling’s point X(24)

Kimberling's point X(24)

Kimberling defined point X(24) as perspector of $\triangle ABC$ and Orthic Triangle of the Orthic Triangle of $\triangle ABC$ .

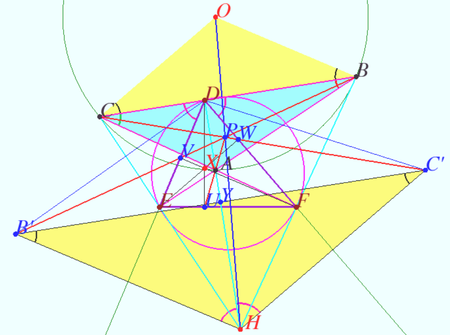
Theorem 1

Denote $T_0$ obtuse or acute $\triangle ABC.$ Let $T_0$ be the base triangle, $T_1 = \triangle DEF$ be Orthic triangle of $T_0, T_2 = \triangle UVW$ be Orthic Triangle of $T_1$ . Let $O$ and $H$ be the circumcenter and orthocenter of $T_0.$

Then $\triangle T_0$ and $\triangle T_2$ are homothetic, the point $P,$ center of this homothety lies on Euler line $OH$ of $T_0.$

The ratio of the homothety is $k = \frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C.$

Proof

WLOG, we use case $\angle A = \alpha > 90^\circ.$

Let $B'$ be reflection $H$ in $DE.$ In accordance with Claim, $\angle BVD = \angle HVE \implies B', V,$ and $B$ are collinear.

Similarly, $C, W,$ and $C',$ were $C'$ is reflection $H$ in $DF,$ are collinear.

Denote $\angle ABC = \beta = \angle CHD, \angle ACB = \gamma = \angle BHD \implies$

$\angle HDF = \angle HDE = \angle DHB' = \angle DHC' = 180^\circ - \alpha.$

$B'C' \perp HD, BC \perp HD \implies BC|| B'C'.$ $OB = OC, HB' = HC', \angle BOC = \angle B'HC' = 360^\circ - 2 \alpha \implies OB ||HB', OC || HC' \implies$

$\triangle HB'C' \sim \triangle OBC, BB', CC'$ and $HO$ are concurrent at point $P.$

In accordance with Claim, $\angle HUF = \angle AUF \implies$ points $H$ and $P$ are isogonal conjugate with respect $\triangle UVW.$

$\angle HDE = \alpha - 90^\circ, \angle HCD = 90^\circ - \beta \implies$

$HB' = 2 HD \sin (\alpha - 90^\circ) = - 2 CD \tan(90^\circ- \beta) \cos \alpha = - 2 AC \cos \gamma \frac {\cos \beta}{\sin \beta} \cos \alpha = - 4 OB \cos A \cos B \cos C.$ $k = \frac {HB'}{OB} = \frac {HP}{OP}= - 4 \cos A \cos B \cos C \implies \frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C.$

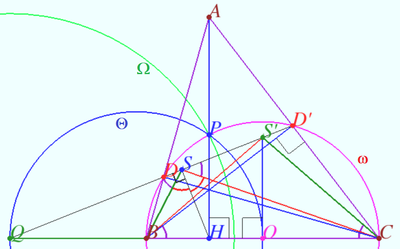
Claim

Let $\triangle ABC$ be an acute triangle, and let $AH, BD',$ and $CD$ denote its altitudes. Lines $DD'$ and $BC$ meet at $Q, HS \perp DD'.$ Prove that $\angle BSH = \angle CSH.$

Proof

Let $\omega$ be the circle $BCD'D$ centered at $O (O$ is midpoint $BC).$

Let $\omega$ meet $AH$ at $P.$ Let $\Omega$ be the circle centered at $Q$ with radius $QP.$

Let $\Theta$ be the circle with diameter $OQ.$

Well known that $AH$ is the polar of point $Q,$ so $QO \cdot HO = QP^2 \implies QB \cdot QC = (QO – R) \cdot (QO + R) = QP^2$ $\implies P \in \Theta, \Omega \perp \omega.$

Let $I_{\Omega}$ be inversion with respect $\Omega, I_{\Omega}(B) = C, I_{\Omega}(H) = O,I_{\Omega}(D) = D'.$

Denote $I_{\Omega}(S) = S'.$

$HS \perp DD' \implies S'O \perp BC \implies BS' = CS' \implies \angle OCS' = \angle OBS'.$ $\angle QSB = \angle QCS' = \angle OCS' = \angle OBS' = \angle CSS'.$ $\angle BSH = 90 ^\circ – \angle QSB = 90 ^\circ – \angle CSS' =\angle CSH.$

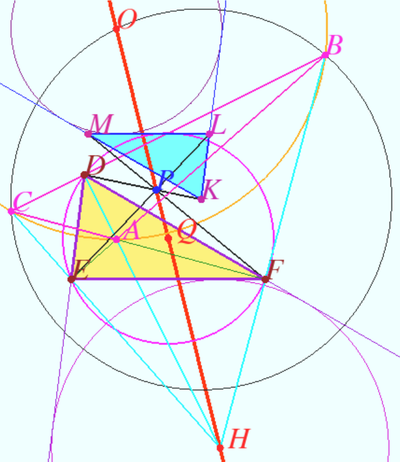
Theorem 2

Let $T_0 = \triangle ABC$ be the base triangle, $T_1 = \triangle DEF$ be orthic triangle of $T_0, T_2 = \triangle KLM$ be Kosnita triangle of $T_0.$ Then $\triangle T_1$ and $\triangle T_2$ are homothetic, the point $P,$ center of this homothety lies on Euler line of $T_0,$ the ratio of the homothety is $k = \frac {\vec PH}{\vec OP} = 4 \cos A \cos B \cos C.$ We recall that vertex of Kosnita triangle are: $K$ is the circumcenter of $\triangle OBC, L$ is the circumcenter of $\triangle OAB, M$ is the circumcenter of $\triangle OAC,$ where $O$ is circumcenter of $T_0.$

Proof

Let $H$ be orthocenter of $T_0, Q$ be the center of Nine-point circle of $T_0, HQO$ is the Euler line of $T_0.$ Well known that $EF$ is antiparallel $BC$ with respect $\angle A.$

$LM$ is the bisector of $AO,$ therefore $LM$ is antiparallel $BC$ with respect $\angle A$ $\implies LM||EF.$ Similarly, $DE||KL, DF||KM \implies \triangle DEF$ and $\triangle KLM$ are homothetic.

Let $P$ be the center of homothety.

$H$ is $D$ -excenter of $\triangle DEF, O$ is $K$ -excenter of $\triangle KLM \implies$ $P \in HO.$

Denote $a = BC, \alpha = \angle A, \beta = \angle B, \gamma = \angle C, R$ circumradius $\triangle ABC.$ $\angle EHF = 180^\circ - \alpha, EF = BC |\cos \alpha| = 2R \sin \alpha |\cos \alpha|.$ $LM = \frac {R}{2} (\tan \beta + \tan \gamma) = \frac {R \sin (\beta + \gamma)}{2 \cos \beta \cdot \cos \gamma} \implies$ $k = \frac {DE}{KL} = 4\cos \alpha \cdot \cos \beta \cdot \cos \gamma \implies$ $\frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C \implies P$ is the point $X(24).$

vladimir.shelomovskii@gmail.com, vvsss

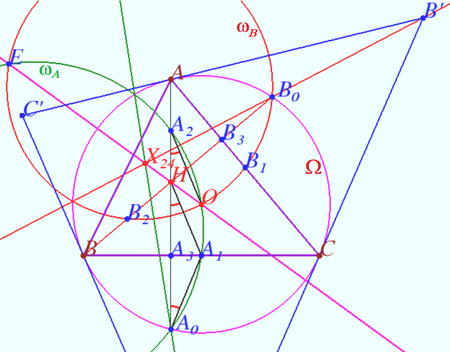
Theorem 3

Let $\triangle ABC$ be the reference triangle (other than a right triangle). Let the altitudes through the vertices $A, B, C$ meet the circumcircle $\Omega$ of triangle $ABC$ at $A_0, B_0,$ and $C_0,$ respectively. Let $A'B'C'$ be the triangle formed by the tangents at $A, B,$ and $C$ to $\Omega.$ (Let $A'$ be the vertex opposite to the side formed by the tangent at the vertex A). Prove that the lines through $A_0A', B_0B',$ and $C_0C'$ are concurrent, the point of concurrence $X_{24}$ lies on Euler line of triangle $ABC, X_{24} = O + \frac {2}{J^2 + 1} (H – O), J = \frac {|OH|}{R}.$

Proof

At first one can prove that lines $A_0A', B_0B',$ and $C_0C'$ are concurrent. This follows from the fact that lines $AA_0, BB_0,$ and $CC_0$ are concurrent at point $H$ and Mapping theorem (see Exeter point $X_{22}).$

Let $A_1, B_1,$ and $C_1$ be the midpoints of $BC, AC,$ and $AB,$ respectively.

Let $A_2, B_2,$ and $C_2$ be the midpoints of $AH, BH,$ and $CH,$ respectively.

Let $A_3, B_3,$ and $C_3$ be the foots of altitudes from $A, B,$ and $C,$ respectively.

The points $A, A_2, H,$ and $A_3$ are collinear. Similarly the points $B, B_2, H, B_3$ and $C, C_2, H, C_3$ are collinear.

Denote $I_{\Omega}$ the inversion with respect $\Omega.$ It is evident that $I_{\Omega}(A') = A_1, I_{\Omega}(B') = B_1, I_{\Omega}(C') = C_1, I_{\Omega}(A_0) = A_0, I_{\Omega}(B_0) = B_0, I_{\Omega}(C_0) = C_0.$

Denote $\omega_A = I_{\Omega}(A'A_0), \omega_B = I_{\Omega}(B'B_0) \omega_C = I_{\Omega}(C'C_0) \implies$ $A_0 \in \omega_A, A_1 \in \omega_A, O \in \omega_A, B_0 \in \omega_B, B_1 \in \omega_B, O \in \omega_B \implies\ O = \omega_A \cap \omega_B \cap \omega_C.$

It is known that $A_2O = HA_1 = A_0A_1, A_2O || HA_1 \implies \angle OA_2A_0 = \angle A_1A_0A_2, OA_1 ||A_0A_2 \implies A_2 \in \omega_A.$

Similarly, $B_2 \in \omega_B, C_2 \in \omega_C.$

We use Claim and get that the power of point $H$ with respect each circle $\omega_X$ is $HA_2 \cdot HA_0 = HB_2 \cdot HB_0 = HC_2 \cdot HC_0 = \frac {R^2 \cdot (1-J^2)} {2}.$

$H = AA_0 \cap BB_0 \cap CC_0 \implies H$ lies on common radical axis of $\omega_A, \omega_B,$ and $\omega_C.$

Therefore second crosspoint of these circles point $E$ lies on line $OH$ which is the Euler line of $\triangle ABC \implies$ $X_{24} = I_{\Omega}(E)$ lies on the same Euler line as desired.

Last we will find the length of $OX_{24}.$ $OH \cdot HE = \frac {R^2 \cdot (1–J^2)} {2}.$ $OE \cdot OX_{24} = (OH + HE)\cdot OX_{24} = R^2.$ $\frac {OX_{24}}{OH} = \frac {R^2}{OH^2 + OH \cdot HE} = \frac {1}{J^2 + \frac {1– J^2} {2}} = \frac {2}{1+J^2},$ as desired.