1999 AIME Problems/Problem 8

Problem

Let $\mathcal{T}$ be the set of ordered triples $(x,y,z)$ of nonnegative real numbers that lie in the plane $x+y+z=1.$ Let us say that $(x,y,z)$ supports $(a,b,c)$ when exactly two of the following are true: $x\ge a, y\ge b, z\ge c.$ Let $\mathcal{S}$ consist of those triples in $\mathcal{T}$ that support $\left(\frac 12,\frac 13,\frac 16\right).$ The area of $\mathcal{S}$ divided by the area of $\mathcal{T}$ is $m/n,$ where $m_{}$ and $n_{}$ are relatively prime positive integers, find $m+n.$

Solution

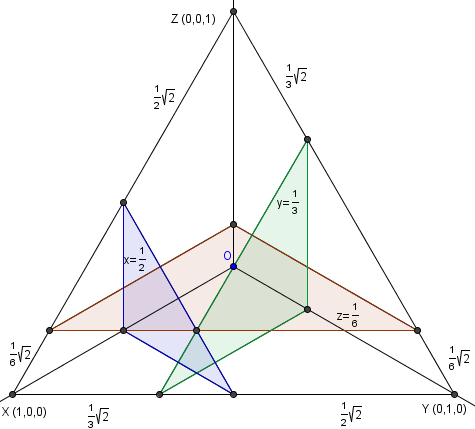
This problem just requires a good diagram and strong 3D visualization.

The region in $(x,y,z)$ where $x \ge \frac{1}{2}, y \ge \frac{1}{3}$ is that of a little triangle on the bottom of the above diagram, of $y \ge {1}{3}, z \ge \frac{1}{6}$ is the triangle at the right, and $x \ge \frac 12, z \ge \frac 16$ the triangle on the left, where the triangles are coplanar with the large equilateral triangle formed by $x+y+z=1,\ x,y,z \ge 0$ . We can check that each of the three regions mentioned fall under exactly two of the inequalities and not the third.

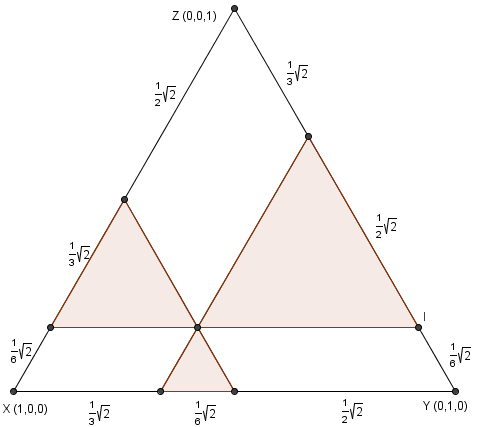
The side length of the large equilateral triangle is $\sqrt{2}$ , which we can find using 45-45-90 $\triangle$ with the axes. Using the formula $A = \frac{s^2\sqrt{3}}{4}$ for equilateral triangles, the area of the large triangle is $\frac{(\sqrt{2})^2\sqrt{3}}{4} = \frac{\sqrt{3}}{2}$ . Since the lines of the smaller triangles are parallel to those of the large triangle, by corresponding angles we see that all of the triangles are similar, so they are all similar triangles. We can solve for their side lengths easily by subtraction, and we get $\frac{\sqrt{2}}{6}, \frac{\sqrt{2}}{3}, \frac{\sqrt{2}}{2}$ . Calculating their areas, we get $\frac{\sqrt{3}}{8}, \frac{\sqrt{3}}{18}, \frac{\sqrt{3}}{72}$ . The ratio $\frac{\mathcal{S}}{\mathcal{T}} = \frac{\frac{9\sqrt{3} + 4\sqrt{3} + \sqrt{3}}{72}}{\frac{\sqrt{3}}{2}} = \frac{14}{36} = \frac{7}{18}$ , and the answer is $m + n = \boxed{025}$ .

To simplify the problem, we could used the fact that the area ratios are equal to the side ratios squared, and we get $\left(\frac{1}{2}\right)^2 + \left(\frac{1}{3}\right^2 + \left(\frac{1}{6}\right)^2 = \frac{14}{36} = \frac{7}{18}$ (Error compiling LaTeX. Unknown error_msg).

1999 AIME (Problems • Answer Key • Resources)
Preceded by Problem 7	Followed by Problem 9
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search

1999 AIME Problems/Problem 8

Problem

Solution

See also